What is the tension in the cable?

[kankerfist]

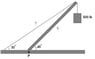
The picture I attached to this thread is a system that I came across while studying for my final exam today. It is a system that is in equilibrium, and the only numerical values are:

Angle of wire/ground: 30
Angle of strut/ground: 45
Mass of hanging weight: 500 lb
Mass of strut: 100 lb (uniform mass)

I have written out all the forces that I can find, several of which are couples that cancel out, but I cannot find a numerical value for the tension in the cable T. The question asks what the tension is, and I have begun to think there is no way to describe tension numerically from the given data. Can someone please help me out by confirming that there isn't enough data here to describe tension numerically? Thanks a lot!

 

[Doc Al]

Seems like there's enough information to me. Have you applied the equilibrium conditions to the strut? (What's the net torque on the strut due to all the forces on it?)

 

[kankerfist]

The net torque at P has to be zero. I guess my problem is that I haven't figured out how to numerically describe the positions of the forces relative to P. For instance, one of the torque forces is the 500 lb weight. I know the direction of the force is straight down, but I'm not sure how to numerically find its position vector relative to P. If I did, then I could calculate the cross product to find the torque due to the 500 lb weight. Thanks for the reply!

 

[Doc Al]

Perhaps you are thinking that you need the length of the strut? If that's the problem, just call the length "L". You'll find that you don't need the numerical value: when you write the torque equation, the length will cancel out.

(Tip: Try to solve the problem symbolically. Wait until the last step before reaching for the calculator.)

 

[PPonte]

I guess my problem is that I haven't figured out how to numerically describe the positions of the forces relative to P. For instance, one of the torque forces is the 500 lb weight. I know the direction of the force is straight down, but I'm not sure how to numerically find its position vector relative to P.

The torque force of the 500 lb weight is applied at the top of the strut and the direction of this force is as you said straight down. Then, you need to find the lever arm.

The lever arm is the perpendicular distance from the axis of rotation to a line drawn along the direction of the force.

Once you know the lever-arm, you may find the torque.
You may follow the same strategy to find the other torques.

Remember Doc Al's hints!

 

[kankerfist]

You guys are about 10x as helpful as my teacher! Here is where I have gotten:
Grav Torques from the masses + Torque from wire's tension = 0,
so:
x_strut is distance from P to the 500lb mass lever arm
x_wire is distance from where the wire is grounded to P
h is the height of where the wire and strut meet

(226.8)(9.8)(x_strut) + (45.36)(9.8)(x_strut / 2) = (Tension)(x_wire)

Then geometrically I know that:
Sin[30] = h/(x_strut + x_wire)
Sin[45] = h/x_strut

so:
h = (x_strut + x_wire)Sin[30] = (x_strut)Sin[45]

Solving for x_wire:
x_wire = 0.414 x_strut

Then plugging into the original torque equation gives me:
(226.8)(9.8)(x_strut) + (45.36)(9.8)(x_strut / 2) = (Tension)(0.414 x_strut)

Solving this for Tension yields 5905 N of tension in the wire. Any hints on whether or not I'm approaching this correctly would be greatly appreciated!

 

[kankerfist]

Actually, I got the lever arm on tension messed up there. Looks like the lever arm of tension is actually (0.414)(x_strut)Sin(30)

This fix yields a tension of 11816 N of tension in the wire

 

[pizzasky]

x_strut is distance from P to the 500lb mass lever arm
h is the height of where the wire and strut meet

To provide a clearer definition, it would be better to say that x_{strut} is the HORIZONTAL distance from P to the vertical wire connecting the 500lb mass. Also, h is the height of the point where the wire and strut meet.

Then geometrically I know that:
Sin[30] = h/(x_strut + x_wire)
Sin[45] = h/x_strut

Really? Check again!

 

[Doc Al]

Here is where I have gotten:
Grav Torques from the masses + Torque from wire's tension = 0,
so:
...
Any hints on whether or not I'm approaching this correctly would be greatly appreciated!

Looks like you have things a bit messed up. Let's do it step by step. (I'll use "L" as the length of the strut.) First, let's find the clockwise torques about point P:
-due to the weight of the strut: (L/2)*(100 lbs)* sin(45)
-due to the hanging mass: (L)*(500 lbs)* sin(45)

Now find the counterclockwise torque about point P, which is due to the tension in the wire. To do that you need to figure out the angle that the wire makes with the strut. It's easy--just use what you know about triangles. I'll call that angle "theta":
-due to wire: (L)*(T) sin(theta)

Once you figure out theta, just set total torque equal to zero (or clockwise torques equal to counterclockwise torques -- same thing) and solve for T.