BatsDude
- 14
- 0
Hi all. Brushing up on some of my force and torque stuff so I can do some modelling in software.
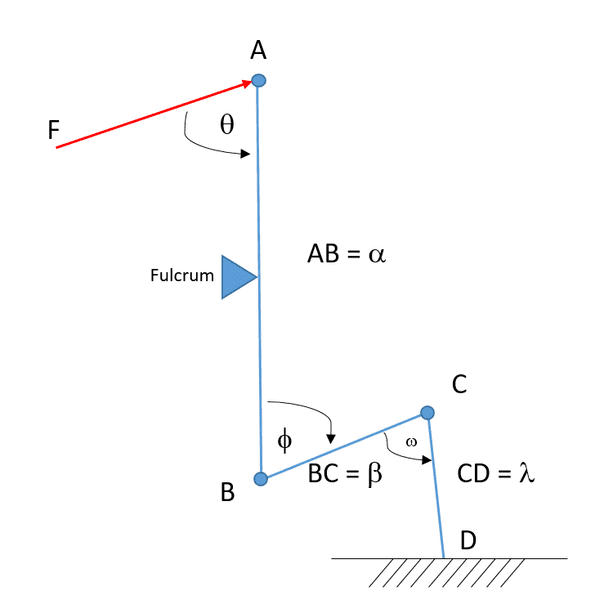
I have a system as shown in the picture. A force F acts at point A, which is the end point of the lever AB. Connected to the lever is a link BC, and connected to BC at point C is another link CD, which is anchored to the ground.
I'm trying to resolve this into a torque around the point D. I know the lengths, and all the angles involved, I'm just confused about how the force travels through the linkage.
T = F*r*sin(theta) is the equation for torque from a force acting at an angle
My attempt was to try and equate the forces through the lever first.
Let F_b be the output force of the lever at point B, resulting from F acting at point A.
F*(alpha/2)*sin(theta) = F_b*(alpha/2) *sin(phi). Solve for F_b.
From here, I would assume that this force F_b is acting on member CD at an angle of omega and at a lever length of lambda. From this I can calculate the torque around D.
However, I'm not at all sure if this is correct.
Homework Statement
I have a system as shown in the picture. A force F acts at point A, which is the end point of the lever AB. Connected to the lever is a link BC, and connected to BC at point C is another link CD, which is anchored to the ground.
I'm trying to resolve this into a torque around the point D. I know the lengths, and all the angles involved, I'm just confused about how the force travels through the linkage.
Homework Equations
T = F*r*sin(theta) is the equation for torque from a force acting at an angle
The Attempt at a Solution
My attempt was to try and equate the forces through the lever first.
Let F_b be the output force of the lever at point B, resulting from F acting at point A.
F*(alpha/2)*sin(theta) = F_b*(alpha/2) *sin(phi). Solve for F_b.
From here, I would assume that this force F_b is acting on member CD at an angle of omega and at a lever length of lambda. From this I can calculate the torque around D.
However, I'm not at all sure if this is correct.