humanino
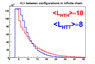
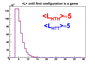
- 2,523
- 8
All right...
Code:
#define HEAD 1
#define TAIL 0
int toss1, toss2, toss3;
int Nicolas, Henry;
int LNicolas, LHenry;
int BNicolas, BHenry;
int nowinner(int Tosses)
{
if (!BNicolas && toss1 == HEAD && toss2 == TAIL && toss3 == TAIL)
{
Nicolas++;
LNicolas += Tosses;
BNicolas = 1;
return 0;
}
if (!BHenry && toss1 == HEAD && toss2 == TAIL && toss3 == HEAD)
{
Henry++;
LHenry += Tosses;
BHenry = 1;
return 0;
}
return 1;
}
int main(int argc, char* argv[])
{
Nicolas = Henry = LNicolas = LHenry = 0;
int Ngames=100000, Tosses;
for(int game=0;game<Ngames;game++)
{
BNicolas=0;
BHenry=0;
toss1 = rand() % 2;
toss2 = rand() % 2;
toss3 = rand() % 2;
Tosses = 3;
/* while(!BNicolas&&!BHenry) */ /* will give 5 and 5 */
while(!(BNicolas&&BHenry)) /* will give 8 and 10 */
{
nowinner(Tosses++);
toss1 = toss2;
toss2 = toss3;
toss3 = rand() % 2;
}
}
printf("Probabilities to win : Nicolas=%2.6f Henry=%2.6f\n",float(Nicolas)/Ngames,float(Henry)/Ngames);
printf("Number of tosses to victory : Nicolas=%2.6f/ Henry=%2.6f\n",float(LNicolas)/Nicolas,float(LHenry)/Henry);
return 0;
}