Total Josephson current through junction with magnetic field

[Mr_Allod]

Homework Statement

Show that the total Josephson current though a Josephson Junction is:
$$d_xd_yj_0 \frac {\phi_0}{2\pi \phi} \left[ \cos(\psi_0) - \cos(\psi_0 + \frac{2\pi \phi}{\phi_0}) \right]$$

Relevant Equations

Total flux through the junction: $\phi = Bd_xd_y$
Current density at position x: $J(x) = j_0\sin(\psi_0 + \frac{2\pi x}{\phi_0}Bd_y)$

Hello there,

I am given a diagram of a Josephson Junction like so:

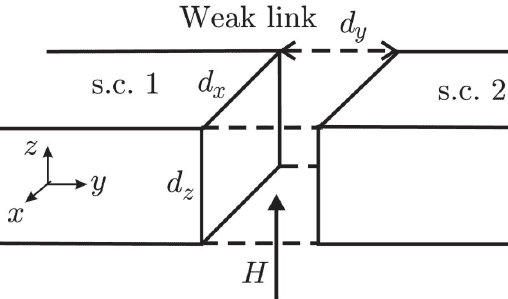
With a magnetic field $B = \mu_oH$ in the z-direction. I'm reasonably sure $d_x,d_y,d_z$ are normal lengths, not infinitesimal lengths although that is up for debate. Using the above equations I rearrange the expression for J(x) to be in terms of $\phi$ and compute the following integral:

$$\int_{\frac {-d_x}{2}}^{\frac {d_x}{2}}\int_{\frac {-d_y}{2}}^{\frac {d_y}{2}} j_0\sin(\psi_0 + \frac{2\pi \phi}{\phi_0d_x}x)d_xd_y$$

This yielded:

$$d_xd_yj_0 \frac {\phi_0}{2\pi \phi} \left[ \cos(\psi_0 - \frac{\pi \phi}{\phi_0}) - \cos(\psi_0 + \frac{\pi \phi}{\phi_0}) \right]$$

Where $\psi_0$ is the phase difference at $x=0$. This is not the same as the expression we were given in the problem but it is quite similar which makes me think I am on the right track. Is there something else I need to do with the expression we are given before integrating to find the total current?

 

[TSny]

$$\int_{\frac {-d_x}{2}}^{\frac {d_x}{2}}\int_{\frac {-d_y}{2}}^{\frac {d_y}{2}} j_0\sin(\psi_0 + \frac{2\pi \phi}{\phi_0d_x}x)d_xd_y$$

Shouldn't the integration be over $x$ and $z$ rather than $x$ and $y$?

Maybe the origin of the coordinate system is such that $x$ ranges from $0$ to $d_x$ rather than from $-d_x/2$ to $d_x/2$ and $z$ ranges from $0$ to $d_z$ rather than from $-d_z/2$ to $d_z/2$.

 

[Mr_Allod]

Shouldn't the integration be over $x$ and $z$ rather than $x$ and $y$?

Maybe the origin of the coordinate system is such that $x$ ranges from $0$ to $d_x$ rather than from $-d_x/2$ to $d_x/2$ and $z$ ranges from $0$ to $d_z$ rather than from $-d_z/2$ to $d_z/2$.

I think you're right on both counts. I suppose if I had paid more attention to the figure I would have realized I'm using the wrong origin. Integrating from $0$ to $d_{x,z}$ gives the right answer. With regards to the area of integration, I think I was just forcing the solution to be in line with the expression we're given and it's entirely possible there was a typo in it. It wouldn't be the first time.