doublemint
- 138
- 0
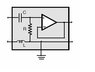
So I am suppose to solve for the transfer function of the circuit i have attached.
First I would find the V_out at the resistor. This is done by V_in=I(jwL + 1/jwC + R)
Then the transfer function is: H(f) = V_out/V_in = R/(jwL + 1/jwC + R)
Now I need to find the transfer function by using the Fourier transform.
Given the boundaries:
h(t) : 0 for t<0
e^(-at)(Acos(w1)t + Bsin(w1)t) for t>=0
so I have done the FT of h(t) to find H(f) = \frac{-A(a+2jf\pi)-2Bf\pi}{4\pi^2f^2 - 4\pi jaf-(a^2+4\pi^2f^2_1)}
rearranging the equation from the beginning:
H(f) = \frac{\frac{wR}{L}}{jw^2 - j\frac{1}{LC} + \frac{wR}{L}}
now when i try to compare the two transfer functions to determine A, B, a, and w1, I cannot seem to determine what 'a' is because it conflicts..
Does anyone see what I did wrong?
DM
First I would find the V_out at the resistor. This is done by V_in=I(jwL + 1/jwC + R)
Then the transfer function is: H(f) = V_out/V_in = R/(jwL + 1/jwC + R)
Now I need to find the transfer function by using the Fourier transform.
Given the boundaries:
h(t) : 0 for t<0
e^(-at)(Acos(w1)t + Bsin(w1)t) for t>=0
so I have done the FT of h(t) to find H(f) = \frac{-A(a+2jf\pi)-2Bf\pi}{4\pi^2f^2 - 4\pi jaf-(a^2+4\pi^2f^2_1)}
rearranging the equation from the beginning:
H(f) = \frac{\frac{wR}{L}}{jw^2 - j\frac{1}{LC} + \frac{wR}{L}}
now when i try to compare the two transfer functions to determine A, B, a, and w1, I cannot seem to determine what 'a' is because it conflicts..
Does anyone see what I did wrong?
DM