Decompose 4x4 determinant into 24 determinants -- How many are zero?

[zenterix]

Homework Statement

The following problem is problem 6 of Chapter 5.2 "Permutations and Cofactors" of Gilbert Strang's "Introduction to Linear Algebra", Fifth Edition

(a) If $a_{11}=a_{22}=a_{33}=0$, how many of the six terms in det A will be zero?

(b) If$a_{11}=a_{22}=a_{33}=a_{44}=0$, how many of the 24 products $a_{1j}=a_{2k}=a_{3l}=a_{4m}$ are sure to be zero?

My question is about solutions to b).

I will show the theory behind the question and also my solutions, and my question is if anyone has a clever solution for b). Such a solution would allow us to extrapolate to n x n without too much work.

Relevant Equations

The context of this problem is the "Big Formula" for computing a determinant.

Given a square matrix, one property of its determinant is that it is a linear function of each row separately.

If we apply this property repeatedly, we can decompose a determinant into a sum of determinants. In fact, for an n x n matrix, there are $n^n$ different such determinants.

Each of those determinants contains only $n$ non-automatically-zero entries.

Here is an example of the decomposition for a 2 x 2 matrix

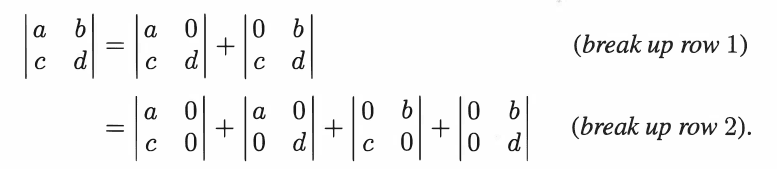
We have $2^2=4$ determinants, each with only #n=2# non-automatically-zero entries. By "non-automatically-zero" I just mean that they aren't zero by default. Of course, any of $a,b,c$, or $d$ can be zero, but that depends on the matrix in question.

Now, two of the determinants above are automatically zero because they contain a zero column.

Turns out that for an n x n matrix, when we decompose the determinant like this, only #n!# of the determinants are potentially non-zero. All the others are automatically zero because of a zero row or column.

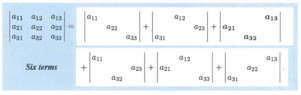
In (a) of the problem, Strang is considering the determinant of a 3 x 3 matrix. After decomposing it using linearity as above, we have 3! determinants which are potentially non-zero. Here they are for illustration

The characteristic common to these determinants is that the non-automatically-zero elements are each in a distinct row and column from the others.

We are essentially saying: we have n elements to place in n rows, and each element must be in a different column. There are n! ways to do this.

Notice that if any of the non-automatically-zero elements in a determinant are in fact zero, then that determinant becomes zero because a zero row and column are introduced. In the picture above, if any of the $a_{ij}$ is zero in any determinant then that determinant is zero.

Okay, so back to the question.
We can see from the picture above, that if $a_{11}=a_{22}=a_{33}=0$ then the non-bold determinants are automatically zero. Hence, the answer to (a) is 4.
My question is about (b).
I solved it in a specific way that I found to be labor-intensive. I am curious about alternative solutions.

Here is my solution
Consider the 4 x 4 determinant

We will have 4! = 24 of the non-automatically-zero determinants, but because the diagonal is all zero, some of these 24 will be zero for sure.

My strategy was to find the ones that are not zero for sure.

If we choose b in the first row as a non-zero element, then pictorially we have

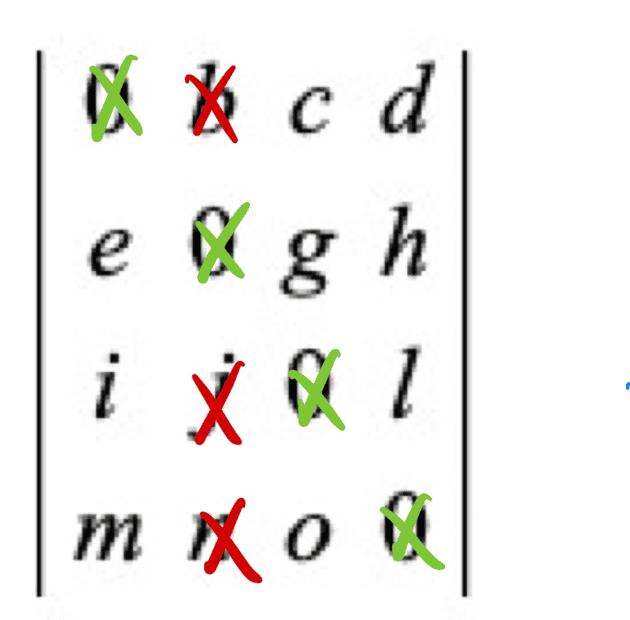
and it seems we can now choose among three options on the second row. However, note that once we choose one on the second row, the third and fourth rows are locked in.

For example,

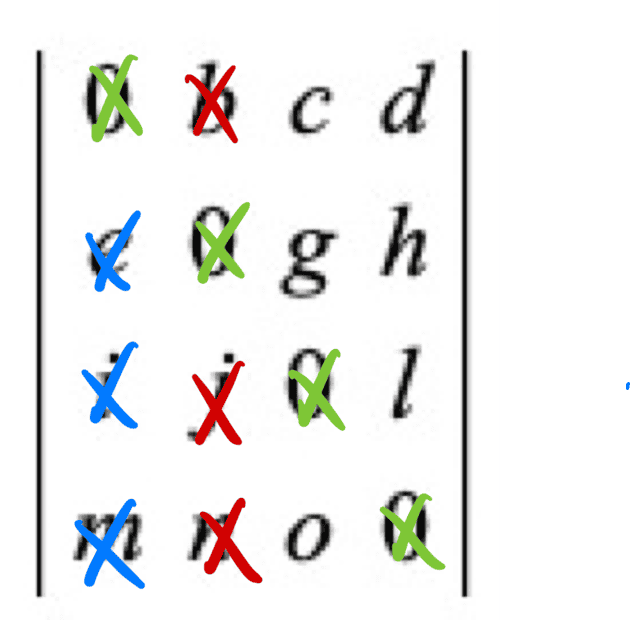
Thus, there are three possible non-automatically-zero determinants when choosing b on the first row.

The same argument applies when choosing c or d on the first row.

Thus we have 9 total non-automatically-zero determinants and so 24 - 9 = 15 that are zero for sure.

This is the answer to (b).

 

[andrewkirk]

We can derive recursive formulas to give us this result for a square matrix of any size.

Let $p_n$ be the number of not-necessarily zero (NNZ) terms in the determinant of a $n\times n$ matrix with the diagonal all zero (call this a type-A matrix).

Let $q_n$ be the number of NNZ terms in the determinant of a $n\times n$ matrix with all but one elements in the diagonal being zero (call this a type-B matrix).

We observe that $p_2=q_2=1$.

For $n>2$ we calculate $p_n,q_n$ in terms of $p_{n-1},q_{n-1}$.
First calculate $p_{n}$, letting $a_{ij}$ denote the element of the matrix in row $i$, column $j$. All terms from the pivot $a_{11}$ are zero because $a_{11}=0$. That leaves $n-1$ nonzero pivots $a_{12}, ..., a_{1n}$, each of which applies to the determinant of a $(n-1)\times(n-1)$ type-B matrix, which has $q_{n-1}$ NNZ terms. So that gives us $(n-1)q_{n-1}$ NNZ terms.

We note that $q_n$ equals $p_n$ plus the number of NNZ terms in the submatrix for pivot $a_{11}$, which we now allow to be nonzero. That submatrix is a $(n-1)\times(n-1)$ type-A matrix, and so has $p_{n-1}$ NNZ terms.

So we have
\begin{align*}
p_n &= (n-1)q_{n-1}\\
q_n &= p_n + p_{n-1}
\end{align*}

Applying the formula gives:
$p_2 =1, q_2=1$
$p_3 = 2, q_3 = 3$
$p_4 = 9, q_4 = 11$
$p_5 = 44, q_5 = 53$
etc

The number of necessarily zero terms will be $n! - p_n$ for a type-A matrix and $n!-q_n$ for type-B.

The result $p_4=9$, which gives $4!-9 = 15$ necessarily zero terms for a type-A $4\times 4$ matrix, agrees with your calc.