Discussion Overview
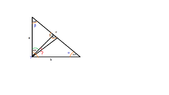
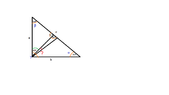
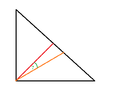
The discussion revolves around calculating the angle between a raised height and an angle bisector in a right-angled triangle, where one angle is specified as 50º. Participants explore the geometric relationships and definitions involved in this scenario.
Discussion Character
- Exploratory
- Mathematical reasoning
- Conceptual clarification
Main Points Raised
- One participant states that the triangle has angles of 90º, 50º, and 40º and seeks to find the angle between the raised height and the angle bisector.
- Another participant expresses confusion over the term "angle follower," suggesting it may not be relevant to the problem.
- A participant clarifies that one line is the angle bisector and the other is drawn from the right angle to the hypotenuse.
- One participant calculates that the angle bisector would be 45º based on the triangle's angles, although they express doubt about the drawing's accuracy.
- Further clarification is provided about drawing lines from the right angle to the hypotenuse and the height line to find the angle between these two lines.
- Another participant suggests that if the angle bisector splits the 90º angle into two 45º angles, the unknown angle between the lines could be 5º.
- A later reply indicates that one participant feels they have understood the problem after the discussion.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the definitions and relationships involved, particularly regarding the term "angle follower" and the accuracy of the drawing. Multiple interpretations of the problem remain present.
Contextual Notes
There are uncertainties regarding the definitions of the lines involved and the accuracy of the geometric representation, which may affect the calculations and conclusions drawn by participants.
