Discussion Overview
The discussion revolves around solving two geometry-related questions involving triangles, specifically focusing on their areas and relationships to other geometric shapes such as circles and squares. The scope includes exploratory reasoning and mathematical reasoning related to area calculations.
Discussion Character
- Exploratory, Mathematical reasoning, Homework-related
Main Points Raised
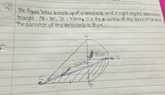
- Some participants propose that if the base and height of two triangles are equal, then their areas must also be equal.
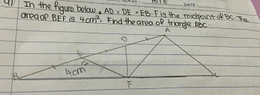
- There is a suggestion to find a larger triangle and subtract areas to solve the problem, although some participants express uncertainty about how to identify this larger triangle.
- One participant mentions using the diameter of a semi-circle to determine the dimensions of the larger triangle.
- Another participant discusses calculating the area of the larger triangle using the formula for the area of a triangle.
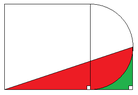
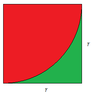
- There is a proposal to take the area of a square and subtract the area of a quarter circle to find a specific area related to the problem.
- A later reply provides a detailed mathematical expression for the area of the larger triangle and the area to be subtracted, leading to a final expression for the area sought in the problem.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to solve the problems, as multiple methods and calculations are proposed, and some uncertainty remains regarding the identification of the larger triangle and the areas involved.
Contextual Notes
Some participants express confusion about how to find certain areas, particularly the "green part," and there are unresolved steps in the calculations presented.