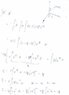- #1
unscientific
- 1,734
- 13
Homework Statement
The problem is attached in the picture. It is to normalize the wavefunction to find the value of A.
The Attempt at a Solution
The solutions used an element volume dV of a very thin shell, then integrated r from 0 to ∞.
I didn't think of this way, I simply integrated using boundaries of ψ, θ and r.
The limits of ψ ranges from 0 to 2∏.
The limits of θ ranges from 0 to 2∏.
The limits of r ranges from 0 to infinity.
However, I get a different answer. I've checked my working through a couple of times, not sure where I went wrong..
Attachments
Last edited: