SUMMARY
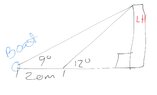
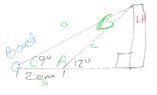
The discussion focuses on solving a trigonometry problem involving a boat and a lighthouse, specifically calculating the distances from the boat to the top of the lighthouse before and after the boat moves. The initial angle of elevation is 9 degrees, and after moving 20 meters forward, the angle increases to 12 degrees. Using the tangent function, the initial distance from the boat to the lighthouse is calculated to be approximately 78.5 meters, while the final distance is about 58.5 meters. The discussion emphasizes the importance of avoiding rounding errors by only rounding at the end of calculations.
PREREQUISITES
- Understanding of trigonometric functions, specifically tangent and cosine.
- Familiarity with angle of elevation concepts.
- Ability to solve equations involving trigonometric identities.
- Basic knowledge of right triangle properties.
NEXT STEPS
- Learn how to apply the Law of Sines in trigonometric problems.
- Study the use of tangent in real-world applications, such as surveying.
- Explore advanced trigonometric identities and their proofs.
- Practice solving similar lighthouse and boat problems using different angles and distances.
USEFUL FOR
Students studying trigonometry, educators teaching mathematical concepts, and anyone interested in applying trigonometric principles to real-world scenarios.