coderot
- 10
- 0
Homework Statement
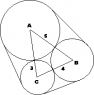
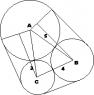
Three cylinders are placed in contact with one another with their axes parallel.
The radii of the cylinders are 3, 4 and 5 cm. An elastic band is stretched around
the three cylinders so that the plane of the band is perpendicular to the axes of
the cylinder. Calculate the length of band that is in contact with the largest
cylinder.
Homework Equations
Sine and Cosine Rules. Properties of circles i.e. arc length and area sector etc. I've also attached an image of what I think this problem looks like.
The Attempt at a Solution
I started this by solving the triangle using the cosine and sine rules. This gave me the following angles: A = 48.2, B = 58.4 and C = 73.4. Note: answers given in degrees.
Now I don't know how to proceed.