- #1
Natasha1
- 493
- 9
Could someone check this for me and help answering the questions at the end
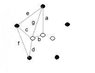
The 3 angles around point 6 are 120 degrees each. This is also the case for point 8 which is linked to point 2, 3 and 7.
Now the 3 angles formed by the lines leaving point 7 are also 120 degrees.
If the distance between point 1 and 2, 2 and 3, 3 and 4, 4 and 5 is 1 cm.
5,6,4 forms an isosceles triangle and so does 2,8,3 triangle.
What is the total distance of the lines?
My answer:
Now, let's start by dropping a vertical line segment 1-7 or a. At point 7, we branch into two lines, one of whom is 7-6 or b. From point 6, we branch into 6-5 or c, and 6-4 or d.
Now, segment a bisects the 108o angle at point 1.
Lets call the side 5-1, e.
In quadrilateral abce, angle 6-5-1 = 360 - 54 - 120 - 120 = 66o.
Lets call side 4-5, f.
In triangle cdf,
Angle 6-5-4 = 108 - 66 = 42o.
So, angle 6-4-5 = 180 - 120 - 42 = 18o.
(This triangle therefore is not isosceles.)
Using the sine rule,
f/sin(120o) = c/sin(18o) = d/sin(42o)
Since f = 1 cm,
c = 1*sin(18o)/sin(120o) = 0.356822 cm.
d = 1*sin(42o)/sin(120o) = 0.772645 cm.
Lets call line segment 1-6, g.
In triangle gce,
Using the cosine rule,
g2 = (c)2 + (e)2 - 2(c)(e)cos(66o)
g2 = (0.356822)2 + (1)2 - 2(0.356822)(1)cos(66o)
g = 0.914908 cm
Using the sine rule,
c/sin (angle 5-1-6) = g/sin(66o)
(0.356822)/sin(angle 5-1-6) = (0.914908)/sin(66o)
So, angle 5-1-6 = arcsin[(0.356822)*sin(66o)/(0.914908)] = 20.872561o
In triangle abg,
g = 0.914908 cm.
Angle 6-1-7 = 54 - 20.872561 = 33.127439o
Angle 7-6-1 = 180 - 33.127439 -120 = 26.872561o
Using the sine rule,
(0.914908)/sin(120o) = a/sin(26.872561o) = b/sin(33.127439o)
So,
a = (0.914908)*sin(26.872561deg)/sin(120o) = 0.477521 cm
b = (0.914908)*sin(33.127439deg)/sin(120o) = 0.577350 cm
Therefore, the total length of the shortest way is:
= a + 2 (b + c + d)
= 0.477521 + 2 (0.577350 +0.356822 +0.772645) = 3.891155 cm.
How can I find the total length in the hexagon (see attached picture)
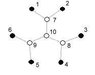
The 3 angles around point 6 are 120 degrees each. This is also the case for point 8 which is linked to point 2, 3 and 7.
Now the 3 angles formed by the lines leaving point 7 are also 120 degrees.
If the distance between point 1 and 2, 2 and 3, 3 and 4, 4 and 5 is 1 cm.
5,6,4 forms an isosceles triangle and so does 2,8,3 triangle.
What is the total distance of the lines?
My answer:
Now, let's start by dropping a vertical line segment 1-7 or a. At point 7, we branch into two lines, one of whom is 7-6 or b. From point 6, we branch into 6-5 or c, and 6-4 or d.
Now, segment a bisects the 108o angle at point 1.
Lets call the side 5-1, e.
In quadrilateral abce, angle 6-5-1 = 360 - 54 - 120 - 120 = 66o.
Lets call side 4-5, f.
In triangle cdf,
Angle 6-5-4 = 108 - 66 = 42o.
So, angle 6-4-5 = 180 - 120 - 42 = 18o.
(This triangle therefore is not isosceles.)
Using the sine rule,
f/sin(120o) = c/sin(18o) = d/sin(42o)
Since f = 1 cm,
c = 1*sin(18o)/sin(120o) = 0.356822 cm.
d = 1*sin(42o)/sin(120o) = 0.772645 cm.
Lets call line segment 1-6, g.
In triangle gce,
Using the cosine rule,
g2 = (c)2 + (e)2 - 2(c)(e)cos(66o)
g2 = (0.356822)2 + (1)2 - 2(0.356822)(1)cos(66o)
g = 0.914908 cm
Using the sine rule,
c/sin (angle 5-1-6) = g/sin(66o)
(0.356822)/sin(angle 5-1-6) = (0.914908)/sin(66o)
So, angle 5-1-6 = arcsin[(0.356822)*sin(66o)/(0.914908)] = 20.872561o
In triangle abg,
g = 0.914908 cm.
Angle 6-1-7 = 54 - 20.872561 = 33.127439o
Angle 7-6-1 = 180 - 33.127439 -120 = 26.872561o
Using the sine rule,
(0.914908)/sin(120o) = a/sin(26.872561o) = b/sin(33.127439o)
So,
a = (0.914908)*sin(26.872561deg)/sin(120o) = 0.477521 cm
b = (0.914908)*sin(33.127439deg)/sin(120o) = 0.577350 cm
Therefore, the total length of the shortest way is:
= a + 2 (b + c + d)
= 0.477521 + 2 (0.577350 +0.356822 +0.772645) = 3.891155 cm.
How can I find the total length in the hexagon (see attached picture)