- #1
RandomMystery
- 69
- 0
I can't understand the sum notation shown in Wikipedia or in this article:
http://mathforum.org/library/drmath/view/53159.html
I want to find the sum notation for (a+b+c)^n
however I can't understand the sum notation:
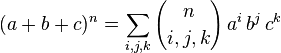
I don't understand the use of brackets or what they mean here and in the binomial theorem.
I think they are what Wikipedia calls the binomial coefficient:
http://en.wikipedia.org/wiki/Binomial_theorem
I also don't understand, is that they are taking the some from i,k,j to what? Shouldn't their be a number on top of the sigma?
I would appreciate the help!
http://mathforum.org/library/drmath/view/53159.html
I want to find the sum notation for (a+b+c)^n
however I can't understand the sum notation:
I don't understand the use of brackets or what they mean here and in the binomial theorem.
I think they are what Wikipedia calls the binomial coefficient:
http://en.wikipedia.org/wiki/Binomial_theorem
I also don't understand, is that they are taking the some from i,k,j to what? Shouldn't their be a number on top of the sigma?
I would appreciate the help!