Triple Product in Laplace Transform

[echandler]

Hello - I'm not sure this is where this should go, but I'm working with Laplace Transforms and differential equations, so this seems as good a place as any. Also, I doubt this is graduate level math strictly speaking, but I went about as high as you can go in calculus and linear algebra during my undergraduate degree, and wouldn't have known where to begin with some of the stuff in this problem.

So I have the equation Int[(x^2)*(e^-sx)*f'(x)dx] on (0,infinity), typical Laplace Transform, except that there is a triple product integration by parts. After hours of integrating by parts and getting nowhere, I made a map of the possible outcomes, shown in the pictures below, and even before asking my teacher if there was some method of figuring out from the map if it had a possible solution by Integration by parts, to which he said he had no idea where to begin with answering that question, I was pretty confident that a solution via integration by parts is not possible. So I though, well, why not write a solution in the form of an infinite series, combine the x^2 term with the series form of e^x term, then, put it back in the integral with f'(x) and now we are back with integration by parts of two functions. Brilliant.

But I have a question. I'm not a mathematician, so forgive me if this is really basic, but if x^2 can be represented by the series: 0*(x^0) + 0*(x^1) + 1*(x^2) + 0*(x^3) + 0*(x^4) + ..., then it can be represented as Sigma[a_n*(x^n)] where n goes from (0,infinity), where a_n = 0 for all n except n=2, where a = 1, then it seems that you can use the Product rule for summations,

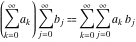, (taken from http://functions.wolfram.com/GeneralIdentities/12/), which to me looks like just a scalar product of two infinite series, and you end up getting only the x^2 terms from each respective series out from the result, because all the other terms in the (x^2) "expansion" are equal to zero and thus "kill" the corresponding terms in the series for the exponential, meaning: (x^2)*exp(x) = (x^4)/2....But this can't really be, can it? I am almost positive I'm missing a fundamental piece of understanding, but I can't seem to determine where I'm going wrong. Please tell me what piece of understanding about series that I am missing!

Thank you in advance.

 

[the_wolfman]

and you end up getting only the x^2 terms from each respective series out from the result

This is not correct. When you have a double summation you have to iterate through each index independently.

For example the sum
$\sum_i \sum_j a_i b_j = a_0b_0 + a_0 b_1 + a_0 b_2 + \dots + a_1 b_0 + a_1 b_1 + a_1 b_2 + \dots + a_2 b_0 + a_2 b_1 + a_2 b_2 + \dots$

In the case where t $a_2 = x^2$ and all other $a_i = 0$ the sum is
$\sum_i \sum_j a_i b_j = 0 + x^2b_0 + x^2 b_1 + x^2 b_2 + \dots = x^2 \sum_j b_j$.

 

[echandler]

Oh wow. That makes so much sense.

Thanks so much!