Trisection of angles-similarly

[bob boben]

The solution of mathematical tasks in the ancient Greek
Trisection of angles
angle=0° - no solution
180°>angle>0° - general solution (consists of 4 parts)

the first part

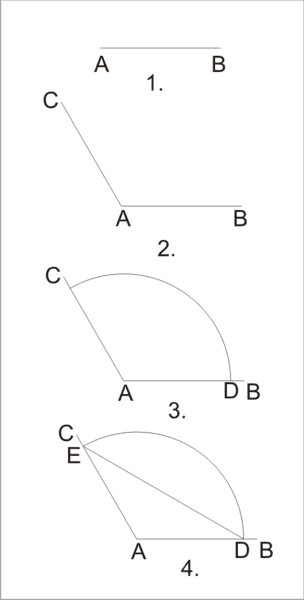
1.ruler AB
2.ruler AC
3.caliper A-AD
4.ruler DE

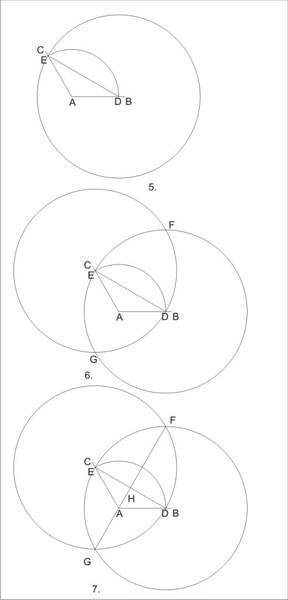
5.caliper D-DE
6.caliper E-DE
7.ruler FG intersects DE the point H ,DH=HE

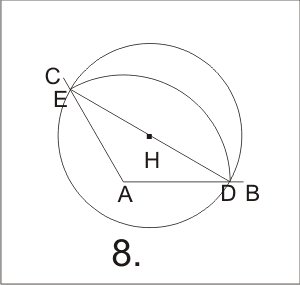
8.caliper H-HE

 

[HallsofIvy]

I'm sorry, I do not understand what you are doing here. I see not even an attempt at "trisecting" angles here. In pictures 1, 2, 3, and 4, you strike an arc on the angle and draw the line through the points where the arc intersects the rays of the angle. In pictures 5, 6, and 7 you construct two circles having the endpoints of the line segment constructed in picture 3 and having that line segment as radius and draw the line through the points of intersection of those circles (so constructing the perpendicular bisector of the line segment and the bisector of the given angle).

Finally, in picture 8, you construct a circle having the line segment you constructed in 4 as diameter. Okay, what lines trisect the original angle?


(It is well known that it is impossible to trisect an angle with straight edge and compasses. That would be equivalent to "constructing" a number that is algebraic of order three and it was long ago proven that the only "constructible numbers" are those that are algebraic of order a power of 2. Of course, one can trisect an angle using other tools.)

 

[bob boben]

I'm sorry, I do not understand what you are doing here. I see not even an attempt at "trisecting" angles here. In pictures 1, 2, 3, and 4, you strike an arc on the angle and draw the line through the points where the arc intersects the rays of the angle. In pictures 5, 6, and 7 you construct two circles having the endpoints of the line segment constructed in picture 3 and having that line segment as radius and draw the line through the points of intersection of those circles (so constructing the perpendicular bisector of the line segment and the bisector of the given angle).

Finally, in picture 8, you construct a circle having the line segment you constructed in 4 as diameter. Okay, what lines trisect the original angle?


(It is well known that it is impossible to trisect an angle with straight edge and compasses. That would be equivalent to "constructing" a number that is algebraic of order three and it was long ago proven that the only "constructible numbers" are those that are algebraic of order a power of 2. Of course, one can trisect an angle using other tools.)

This is the first part, there are three parts, when you look at all four of you will see that it can , we see the 20-30h

 

[Dickfore]

Hey, OP, do you know that a guy called Pierre Wantzel proved it is impossible to do what you are trying to do in 1837?

 

[SteveL27]

Hey, OP, do you know that a guy called Pierre Wantzel proved it is impossible to do what you are trying to do in 1837?

Not so. Note that a ruler is different than a straightedge. A ruler is a straightedge with a known distance marked on it. There are constructions that are possible with ruler and compass that are impossible with straightedge and compass. You can trisect an arbitrary angle with ruler and compass; but of course not straightedge and compass.

Archimedes actually demonstrated the trisection of an angle with ruler and compass.

Here is the reference.

Another means to trisect an arbitrary angle by a "small" step outside the Greek framework is via a ruler with two marks a set distance apart.

http://en.wikipedia.org/wiki/Angle_trisection#With_a_marked_ruler

The OP used the word "ruler," so it's important to make this distinction; because in geometrical constructions, a ruler is much more powerful than a straightedge.

A lot of the online references are similarly confused, using "ruler" when they should say "straightedge."

Repeat: Using ruler and compass, one can trisect an angle. You can win a bar bet with that one. Depending on the bar, of course.

 

[Dickfore]

One can always make a straightedge a ruler by using a compass, so I find it hard to believe what you are saying.

 

[SteveL27]

One can always make a straightedge a ruler by using a compass, so I find it hard to believe what you are saying.

Hard to believe only because it's not very well known. As linked above, Archimedes showed how to trisect an arbitrary angle using ruler and compass; where a ruler is a straightedge with a known distance marked on it. I don't know any more about this than the Wiki reference; but I also remember reading about this years ago.

Here's another reference.

http://en.wikipedia.org/wiki/Neusis_construction

A neusis construction might be performed by means of a 'Neusis Ruler': a marked ruler that is rotatable around the point P

...

Neuseis have been important because they sometimes provide a means to solve geometric problems that are not solvable by means of compass and straightedge alone. Examples are the trisection of any angle in three equal parts, or the construction of a regular heptagon. Mathematicians such as Archimedes of Syracuse (287–212 BC) freely used neuseis. Nevertheless, gradually the technique dropped out of use.

Being allowed to mark distances on the straightedge dramatically alters the nature of what is constructible. This has been known since ancient times. It's only recently that people have forgotten that rulers and straightedges are different things.

I'm afraid I don't know how to respond to your specific point about using the compass to mark a fixed distance on the straightedge.

Evidently Conway was interested in this too.

A geometric construction, also called a verging construction, which allows the classical geometric construction rules to be bent in order to permit sliding of a marked ruler. Using a Neusis construction, cube duplication, angle trisection, and construction of the regular heptagon are soluble. The conchoid of Nicomedes can also be used to perform many Neusis constructions (Johnson 1975). Conway and Guy (1996) give Neusis constructions for the 7-, 9-, and 13-gons which are based on angle trisection.

http://mathworld.wolfram.com/NeusisConstruction.htmlHere is an entertaining article by Underwood Dudley on trisector cranks.

http://web.mst.edu/~lmhall/WhatToDoWhenTrisectorComes.pdf

I found one paragraph particularly revealing. Mathematics Magazine responded to one trisector crank as follows:

This has long ago been proved impossible with an ungraduated ruler and compass alone. [My emphasis]

It's rare for anyone to explicitly make that crucial distinction.

 

[HallsofIvy]

One can always make a straightedge a ruler by using a compass, so I find it hard to believe what you are saying.

No, you cannot move a compass with the straightedge.

 

[bob boben]

second part

9.caliper D-DH , gets the point D1
10.straightedge (ruler) HD1
11.caliper D-DH
12.caliper D1-D1D
13.straightedge ( ruler ) HI1 , gets the point D2

14.caliper D2-D2D
15.caliper D-DD2
16.straightedge (ruler) HI2 , gets the point D3
17.caliper D3-D3D
18.caliper D-DD3
19.straightedge (ruler) HI3 , gets the point D4
20.caliper D4-D4D

21.caliper D-DD4
22.straightedge (ruler) HI4 , gets the point D5
23.this procedure with a compass and a ruler is actually a series of numbers (finite, infinite)

 

[HallsofIvy]

Okay, you have now posted a total of 23 pictures and I must ask "what is your point"? You have, I guess, constructed a 120 degree angle and bisected that to get a 60 degree angle, bisected that to get a 30 degree angle, bisected that to get a 15 degree angle, bisected that to get 7 degree 30 minute angle, and then, apparently, proclaimed that you could continue that to get any angle with degree measure $120/2^n$.

Well, of course. Any one can do that. Bisection of angles is taught in basic secondary school geometry. Where are the trisections you promised?

 

[Dickfore]

Maybe he is using:
$$\frac{1}{3} = \frac{1}{2^{2}} + \frac{1}{2^{4}} + \ldots + \frac{1}{2^{2 n}} + \ldots$$
so he will keep bisecting till infinity and then add the infinite number of contributions to get a third.

 

[Dickfore]

Hard to believe only because it's not very well known.

No, you cannot move a compass with the straightedge.

It is always possible to graduate a straightedge into an arbitrary (but finite) number of graduations by using a straightedge and compass by using a corollary to http://en.wikipedia.org/wiki/Intercept_theorem#Dividing_a_line_segment_in_a_given_ratio" from elementary geometry.

Would someone please define what you mean by a ruler?

 

[Dadface]

It is always possible to graduate a straightedge into an arbitrary (but finite) number of graduations by using a straightedge and compass by using a corollary to http://en.wikipedia.org/wiki/Intercept_theorem#Dividing_a_line_segment_in_a_given_ratio" from elementary geometry.

Would someone please define what you mean by a ruler?

To keep in the spirit of the original problem as considered in ancient Greece the straight edge must be unmarked.

 

[bob boben]

third part
computer program-coreldraw 13
http://www.fileserve.com/file/sZpPSyf/T ... -DOKAZ.cdr
png image
http://www.fileserve.com/file/EpEKHxx/p ... ection.png
the picture is
-circle
-diameter circle AB
-points on the diameter of the circle A(0°),B(180°), C (AD=DC=CB) , D , F(center of the circle ,FB-radius circle)
-tendon EF

I went from the assumptions that there are lines in a circle which is the first point (180 °> point> 0 °), the last point is (360 °> point> 180 °) to the intersection with the circle diameter (AB) be the point C (D).
I shared a circle with corners (second part , 9 to 23).
I found the string (EF, 3.75 ° -187.5 °) which passes through the point C ,which means that we have the angle trisection.
fourth part

24.caliper D-DD5-(22.)
25.caliper E-DD4-(19.)
26.straightedge (ruler) D4D5 , gets the point H1
27.straightedge (ruler) AH1
28.caliper H1-H1D , gets the point H2
29.straightedge (ruler) AH2

 

[bob boben]

angle=180°

30.straightedge (ruler) AB
31.caliper C-CD
32.caliper D-DC ,gets the point E
33.straightedge (ruler) CE
34.caliper E-ED , gets the point F
35.straightedge (ruler) CF

 

[HallsofIvy]

Okay, we've gone on to 35 pictures now and I still have no idea what you are doing. Some words would be nice!

 

[Nowhere Man]

I've chased bob bobur here from BAUT, where his thread was closed because he was spamming it over many different forum websites. Let's see if I can summarize this mess.

In part one, he establishes angle CAB. Selecting point D on line AB (but not explaining how D is chosen), he strikes a circular arc to point E on CD. Finally, he bisects DE (with needless elaboration) at H, and uses H as the center of a circle with radius HD.

In part two, he constructs a 60-degree angle D₁HD. Then he bisects that angle 4 times, producing D₅HD, a 3.75-degree angle. Note that, in all of this, the original angle CAB is ignored.

In part three, things become opaque. Literally, because the two links to the CDR and PNG files are broken. It looks like he pasted them as text from some other message board, which uses ellipses to shorten long URLs. Moving on...

In part four, the whole thing falls apart. Using points D₅ and (I assume) the diametrical projection of D₄, he strikes a line that crosses ED at H₁. Point H₂ is (I believe) the same distance from H₁ as D is. Finally, lines are drawn from A to H₁ and H₂.

If this is the trisection, it is a total failure, because CAH₂, H₂AH₁, and H₁AD are all visibly different angles.

And as a coda, in post 15 he "trisects" a 180-degree angle. I have no idea what that is supposed to prove.

Bob, even if you're not done with part four, you're wasting your time and ours, not just here but on many other boards. It has been proven that, except in a very few special cases, trisection of an angle is impossible. Here are some links you should read thoroughly.

http://www.jimloy.com/geometry/trisect.htm"
http://mathworld.wolfram.com/AngleTrisection.html"
http://en.wikipedia.org/wiki/Angle_trisection"

Fred

 

[HallsofIvy]

Thanks. That explains a lot.
Thread Closed.