Prove that ##AE=2BC## -Deductive Geometry

[chwala]

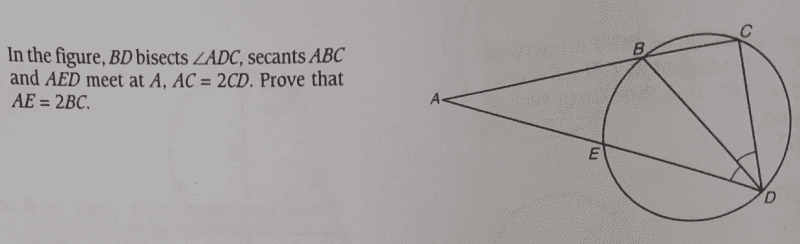
Homework Statement

See attached

Relevant Equations

Geometry

This is the textbook question. I do not have the solution. I am pretty stuck on this one

My attempt on this...find my rough sketch here;

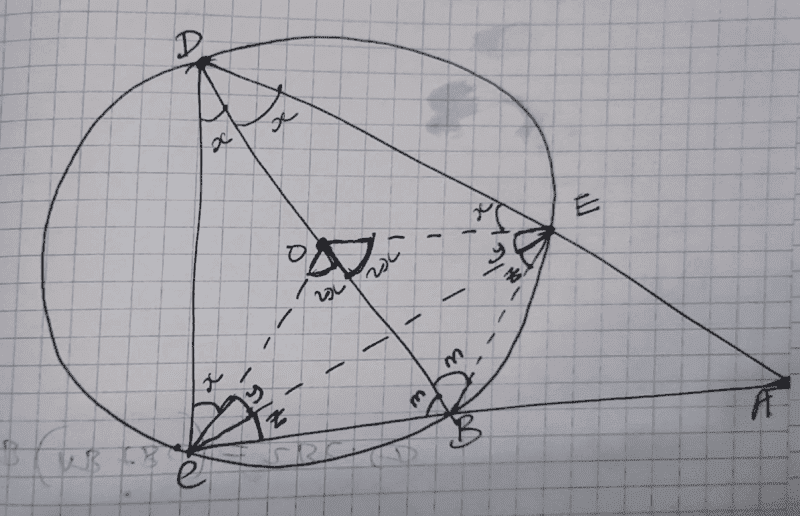
From my analysis;
$x+x+m+m=180^0$ angles opposite each other on a cyclic quadrilateral... I have point $O$ as the centre of the circle.

$x+y+z+x+y+z=180^0$

$⇒2(x+y+z)=180^0, x+y+z=90^0$ therefore $∠DEB= ∠AEB = 90^0$

Also i know that;

$AB⋅AC= AE⋅AD$

 

[anuttarasammyak]

As
BC=BE
We should prove
\triangle DCA \sim \triangle BEA

 

[chwala]

I do not seem to get it...from my analysis;

I let the radius $OD=OB=OE=OC=1$unit.

Therefore; $BD=2$units.

$∠ODC=∠ODE=30^0$ each.

$∠(x+y+z)= 90^0, ∠y=∠z=30^0$each, $∠m=60^0$

$∠OCBE$ is a Rhombus of side $1$ unit.



$\sin 30^0= \dfrac{BC}{BD}$

$0.5= \dfrac{BC}{2}⇒BC=1$unit.

$∠AEB= 90^0$

$∠BAE=30^0$ therefore $\sin 30^0= \dfrac{BE}{AB}$

$0.5= \dfrac{1}{AB}⇒AB=2$unit.

We know from pythagoras theorem that $AE^2+BE^2=AB^2$

$AE=\sqrt{3}$ which does not conform to what we want. Am i missing something here?

 

[chwala]

...Maybe it ought to be $AB= 2BC$

 

[anuttarasammyak]

As
BC=BE
We should prove
\triangle DCA \sim \triangle BEA

We see
\angle ABE=\angle CDE
by drawing OE,OB and OC where O is center of the circle, which is not on BD,with attention to
\angle BOE = \angle BOC = 2 \angle BDE
OB=OE=OC

 

[chwala]

We see
\angle ABE=\angle CDE
by drawing OE,OB and OC where O is center of the circle, which is not on BD.

I have no dispute on this...my working has factored in all that...

 

[chwala]

We see
\angle ABE=\angle CDE
by drawing OE,OB and OC where O is center of the circle, which is not on BD,with attention to
\angle BOE = \angle BOC = 2 \angle BDE
OB=OE=OCView attachment 315334

Are you of the opinion that $AE= 2BC$? As is indicated?

 

[anuttarasammyak]

Yes. More in general
\frac{AC}{CD}=\frac{AE}{EB}
for not only 2 but any ratio value.

 

[Lnewqban]

 

[chwala]

View attachment 315339

Phew man! How were you able to determine the angles?

 

[Lnewqban]

Phew man! How were you able to determine the angles?

AutoCAD does it for me.
I have been trying to make it work with different angles, but so far it does not comply with the identities.
I will keep trying tomorrow.

 

[chwala]

AutoCAD does it for me.
I have been trying to make it work with different angles, but so far it does not comply with the identities.
I will keep trying tomorrow.

Cheers @Lnewqban ...smart!

 

[chwala]

View attachment 315339

...still a problem there...$AE≠2BC$

 

[Lnewqban]

...still a problem there...$AE$ is NOT twice $BC$

Exactly!
That is why more work is needed.
If angle ACD is a 90, then angle EAB must be the arctan of 0.5 (as AC=2CD).
However, that does not work either.

 

[Lnewqban]

 

[chwala]

Looking at it again...in my opinion i tend to think the concept being tested on this question is congruency. In answering this question it is paramount to use a given circle property.

Using the original diagram as shown in post $1$ for our understanding/view, I may state as follows;

$ΔABE$ is congruent to triangle $ΔDBE$.

$∠BEA=∠BED=90^0$.

(Refer to my post $3$ for the calculations on the numerical values given below)

Considering line $BE$ as the line of symmetry and knowing that $BC=BE=1$ unit then

$⇒AB=DB=2$units and

$⇒AE=DE=\sqrt{3}$units.

Clearly, the textbook has a mistake! The correct statement should have been

Prove $AB=2BC$.

 

[anuttarasammyak]

View attachment 315341

I take it as an approximation because tan 64 degrees = 2.05030384158... $\neq$ 2.

[EDIT] We should take it arctan 2 for the exact solution.

Clearly, the textbook has a mistake!

I would like to know how you feel skeptic on my post #5.

 

[chwala]

We see
\angle ABE=\angle CDE
by drawing OE,OB and OC where O is center of the circle, which is not on BD,with attention to
\angle BOE = \angle BOC = 2 \angle BDE
OB=OE=OCView attachment 315334

According to me the centre of the circle i.e point $O$ is on the line $BD$ but according to you it is not. Of course, i could be wrong!

 

[anuttarasammyak]

Some thoughts on a way to measure the lengths in general configuration.

O: unit circle with B,E,C.D on it. In cartesian coordinates
$B(1,0),E(cos \theta, sin\theta),C(cos\theta,-sin\theta),D(cos\phi,sin\phi)$

Equation of line BC: $y=\frac{sin\theta}{1-\cos\theta}(x-1)$

Equation of lne DE: $y-\sin\theta = \frac{\sin\theta-\sin\phi}{\cos\theta-\cos\phi}(x-\sin\theta)$
Thus
A(\frac{\sin\theta(1-\frac{\sin\theta-\sin\phi}{\cos\theta-\cos\phi})+\frac{\sin\theta}{1-\cos\theta}}{\frac{sin\theta}{1-\cos\theta}-\frac{\sin\theta-\sin\phi}{\cos\theta-\cos\phi}}, \frac{\sin\theta}{1-\cos\theta} \frac{\sin\theta(1-\frac{\sin\theta-\sin\phi}{\cos\theta-\cos\phi})+\frac{\sin\theta}{1-\cos\theta}}{\frac{sin\theta}{1-\cos\theta}-\frac{\sin\theta-\sin\phi}{\cos\theta-\cos\phi}} - \frac{\sin\theta}{1-\cos\theta} )

By them we can get formula of side length of triangles in general configuration.

 

[anuttarasammyak]

According to me the centre of the circle i.e point O is on the line BD but according to you it is not. Of course i could be wrong.

"O is on BD or not" and "the ration of 2" have nothing to do with my proof. That may be so for the ratio "2", may be not, and may be so for the ratio "3", may be not and so on.

 

[chwala]

We see
\angle ABE=\angle CDE
by drawing OE,OB and OC where O is center of the circle, which is not on BD,with attention to
\angle BOE = \angle BOC = 2 \angle BDE
OB=OE=OCView attachment 315334

I was reacting to the highlighted and not your proof.

 

[chwala]

"O is on BD or not" and "the ration of 2" have nothing to do with my proof. That may be so for the ratio "2", may be not, and may be so for the ratio "3", may be not and so on.

Noted man. Cheers

 

[anuttarasammyak]

So did you find that O is on BD in the condition of the problem ? I am intereseted in such a coincidence for me.

 

[chwala]

So did you find that O is on BD in the setting of the problem ?

Hi @anuttarasammyak. I do not seem to get you...the question is as it is from the textbook...i am looking at the problem just the same way you're looking at it.

I am not sure if point $O$ i.e the centre of the circle lies on line $BD$.

In such questions like i indicated earlier in my post $16$, one has to apply the properties of the circle in answering the question. That is the start point i guess...that could be a herculian task if we go with your approach of say, taking point $O$ not lying on the line $BD$. With my approach, it could be straightforward as we are dealing with standard angles as shown in my previous post $3$ and $16$.

 

[anuttarasammyak]

O is center point of the circle.

[EDIT] Now I come to an idea that we can choose the configuration of diameter BD by adjusting circumference angles if we may in order to satisfy the ration of the sides given.

 

[Lnewqban]

I take it as an approximation because tan 64 degrees = 2.05030384158... $\neq$ 2.
...

It is only the resolution with which the software represents the angles; I could increase it later to show that the angle's values are exactly what should be to satisfy the 1:2 proportion of the sides of the triangles.

That last drawing shows two 1:2 proportion sides in red for one triangle and two sides in magenta for the other triangle.

Rather than starting with angles, I followed the description of the problem: two secants and one bisector.
Then, I draw the green circle using three points of reference (B, C and D), not knowing where the center would located at.
The green and the dashed circles both pass by point E naturally.

The only liberty I took was assuming the 90 degree angle.
For any combination, the bisector passes by the center of the circle, which makes the top lines symmetrical (note dashed line circle).

 

[chwala]

It is only the resolution with which the software represents the angles; I could increase it later to show that the angle's values are exactly what should be to satisfy the 1:2 proportion of the sides of the triangles.

That last drawing shows two 1:2 proportion sides in red for one triangle and two sides in magenta for the other triangle.

Rather than starting with angles, I followed the description of the problem: two secants and one bisector.
Then, I draw the green circle using three points of reference (B, C and D), not knowing where the center would located at.
The green and the dashed circles both pass by point E naturally.

The only liberty I took was assuming the 90 degree angle.
For any combination, the bisector passes by the center of the circle, which makes the top lines symmetrical (note dashed line circle).

You may have a valid point...but remember this is a textbook question that may not warrant use of software in a class setting. In other words, how would students show the proof as required?

 

[anuttarasammyak]

Rather than starting with angles, I followed the description of the problem: two secants and one bisector.
Then, I draw the green circle using three points of reference (B, C and D), not knowing where the center would located at.
The green and the dashed circles both pass by point E naturally.

The only liberty I took was assuming the 90 degree angle.

Thanks for the explanation. I am not sure and interested in whether we can always choose 90 degree angle configuration, i.e. BD is diameter of the circle, for not only 2 but any given ratio of the sides by adjusting circumference angles. It may be.

 

[Lnewqban]

You may have a valid point...but remember this is a textbook question that may not warrant use of software in a class setting. In other words, how would students show the proof as required?

I don't know how to prove it, reason for which I have used a drawing at scale.
This time, I started from a 2-unit horizontal line followed by a 1-unit vertical line (ACD magenta lines), and ended up with a 1:2 proportion red lines.
Therefore, at least two of the formed triangles must be proprtional (1:2 sides plus one similar angle).

 

[Lnewqban]

@anuttarasammyak , attached is the same drawing, with improved resolution for the angles and measurements of the sides of the triangles.

 

[chwala]

@anuttarasammyak , attached is the same drawing, with improved resolution for the angles and measurements of the sides of the triangles.
View attachment 315404

Nice ...what's your ultimate goal/intention on having different drawings on the problem? are the measurements of $AE$ and$BC$ tending towards the envisaged value? Or drifting away...cheers.

 

[SammyS]

Looking at it again...in my opinion i tend to think the concept being tested on this question is congruency. In answering this question it is paramount to use a given circle property.

. . .

Clearly, the textbook has a mistake! The correct statement should have been

Prove $AB=2BC$.

I agree with @anuttarasammyak .

The textbook problem is solvable.

As he said, you simply need to show that $\displaystyle \triangle DCA \sim \triangle BEA$ . From this you get that $AE=2EB$ .

Also, point $O$ is not necessarily on $BD$ .

 

[chwala]

I agree with @anuttarasammyak .

The textbook problem is solvable.

As he said, you simply need to show that $\displaystyle \triangle DCA \sim \triangle BEA$ . From this you get that $AE=2EB$ .

Also, point $O$ is not necessarily on $BD$ .

Kindly find my rejoinder...sorry am a bit busy had to scribble my response.
I have made use of similarity (on the diagram) as is suggested...and I still cannot see how $BC= EB$.

 

[anuttarasammyak]

There is no mention in the problem that $\angle ACD$ is rectangle or BD is diameter. BD can be a diameter as @Lnewqban showed. But it is not a requirement coming from AC = 2CD that BD is a diameter.

 

[chwala]

View attachment 315462
There is no mention in the problem that $\angle ACD$ is rectangle or BD is diameter. AC = 2CD does not require that BD is a diameter.

If indeed it's not a diameter then we cannot talk of Similarity. That would mean that we are looking at the other option of Congruency. In that case, it would be interesting to see which postulate applies.

 

[anuttarasammyak]

What similarity are you worrying about ?

As
BC=BE
We should prove
\triangle DCA \sim \triangle BEA

This similarity holds with no regard to BD is a diameter or not.

 

[chwala]

What similarity are you worrying about ?This similarity holds with no regard to BD is a diameter or not.

Ok then, can you show how $BC=BE$? Can you draw a sketch of your diagrams separately for clarity.

 

[chwala]

I do not need BC=BE for the similarity. Instead, I used equality of two corresponding angles.

This means you're not in agreement with post $30$. Does the diagram depict the problem? I used it in my analysis.
Is $BE$ equal to $BC$ as indicated?if so, is my analysis correct as shown on post $33$?

 

[anuttarasammyak]

I think @Lnewqban showed us a nice drawing solving the problem with an additional condition of "BD is a diameter".

 

[chwala]

Can we share the idea that two triangle are Similar if two corresponding angles are same ?

A sketch of your similar triangles would be adequate. Thanks.

 

[anuttarasammyak]

Is $BE$ equal to $BC$ as indicated?if so, is my analysis correct as shown on post $33$?

Arc BE and Arc BC have same angle of circumference or central angle. Their length are equal thus BE=BC.

I apologize saying "I do not need BE=BC" and "congruence and similarity" in error.

 

[Lnewqban]

Nice ...what's your ultimate goal/intention on having different drawings on the problem?

No specific goal or intention.
Just trying to understand the problem, which results interesting to me.
The first drawing was the result of beginning with assumed angles: it did not work.
The second drawing was the result of beginning with the information given in the text of the problem: it worked.
The third drawing is exactly as the second one, only showing the value of the resulting angles with a resolution of 0.00, so @anuttarasammyak could see that those values correspond to the 1:2 proportion of the sides of the triangles.

... are the measurements of $AE$ and$BC$ tending towards the envisaged value? Or drifting away...cheers.

AE (1.24 units) is twice as long as BE (0.62 units).
The discontinuos-line circle shows us that the lenghts of BE and BC are exactly the same.

 

[Lnewqban]

I understand that the graphic way is not the way for any student to prove what the problem requires to be proved, as you stated before.
The problem is that I don't know enough math or trigonometry to prove it mathematically.
I hope that my drawings help you gentlemen to find a way to do so, as they prove that the problem is properly stated and that is solvable.

 

[chwala]

I understand that the graphic way is not the way for any student to prove what the problem requires to be proved, as you stated before.
The problem is that I don't know enough math or trigonometry to prove it mathematically.
I hope that my drawings help you gentlemen to find a way to do so, as they prove that the problem is properly stated and that is solvable.

I appreciate your input @Lnewqban ...i would appreciate it if you may have/draw the two similar triangles side by side. That is what i asked for in post $40$...

or alternatively,

tell me what is wrong in my sketch i.e post $33$ as the analysis is directly drawn from your graph drawing of your post $30$.
Cheers bro.

 

[chwala]

@anuttarasammyak , attached is the same drawing, with improved resolution for the angles and measurements of the sides of the triangles.
View attachment 315404

Your diagram looks accurate and convincing! Just one question, i thought for similar Triangles we need to have two pair of corresponding angles which is not the case in your diagram...

you have $90^0, 26.57^0, 63.43^0$ on one triangle and $90^0, 31.72^0,58.28^0$ on the other triangle.

Otherwise, if we were to go with your diagram, then the assertion $AE=2BC$ is correct.

 

[anuttarasammyak]

Please find below my rough hand drawing of the problem. It happens to be the case of
AC/CD = AE/BC = about 0.8. O is outside DE.
May I understand that you say the ratio 2 is the special case that O must be on BD ?

 

[chwala]

Please find below my rough hand drawing of the problem. It happens to be the case of
AC/CD = AE/BC = about 0.8. O is outside DE.
May I understand that you say the ratio 2 is the special case that O must be on BD ?
View attachment 315472

nice @anuttarasammyak ... looks like after all... $AE≠2BC$...rather;

From your analysis; $AE=\dfrac{4}{5}BC$

 

[Steve4Physics]

May I chip in.

Although the diagram makes BD look like it might be a diameter, there is no reason to assume it is (as I think has already been noted).

Consequently, we can’t assume things like ∠EBD = ∠CBD or that ∠BCD = 90º.

There is nothing wrong with the problem statement.

If you are familiar with certain theorems, the solution is straightforward.

The intersecting secants theorem tells us that:
AB•AC = AE•AD.

The angle bisector theorem tells us that:
AD•BC= CD•AB

We are given AC = 2CD.

Proving that AE=2BC requires only simple algebra using the above equations.

 

[anuttarasammyak]

The essence of the problem is
AC/CD=AE/BC
coming from same arc lengths and similarity of triangles.

I draw another case which happens to have the ratio of about 2.4 and a procedure to find the case of ratio 2. With fixed B and D, O keeps out of BD.

 

[Steve4Physics]

FWIW, I agree with @anuttarasammyak.

BD does not need to be a diameter for the 'similarity' approach to be valid.

This follows from the "Angles of Intersecting Chords Theorem". E.g. see https://www.varsitytutors.com/hotmath/hotmath_help/topics/angle-of-intersecting-chords-theorem

The arc length depends on the angle between the chords.

The angle between DC and DB is the same as the angle between DE and DB. (With E being the point of ‘intersection’ of these 3 chords). If follows that arc length BC = arc length BE.