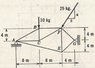
arestes
- 84
- 4
Homework Statement
Find force in members EA, EF and EG given the loads shown. A and G are pinned supports.
Homework Equations
Three equations of equilibrium for sections (method of sections) 2 equations for any node (method of joints).
I also used the dimensions to decompose member forces.
The Attempt at a Solution
I started by analyzing the entire truss to get something about the reactions. I found both VERTICAL components of A and G to be 13 kg-f and 17 kg-f respectively, the horizontal components fulfill : $$A_x + G_x =15 $$
Then I made a cut through BF, CF and AE and evaluated moments about F to get:
$$ \frac{32}{\sqrt{17}}AE=128-4A_x$$
All my other attempts involve the other unknowns and I can't still get them together. What would be the quickest way without throwing in a bunch of equations till I finally reach the answer?
*** I need to teach this and I can't see the "trick" if there is one, so I can teach whatever that trick is supposed to tell me.
BTW,I put this onto an android app and got the solutions. It was painful to input all the data. Do you recommend a particular app or program for these problems?