Undergrad Truth, lie and random confusion

[Taylor_1989]

So I am very, very new to logic based questions, and in the past have solved some with relative ease but whilest scrolling through the next to find some example stuff I came across a website that gives a question and hints to the question if stuck, so I thought this would be good practice. But came to realize I was getting stuck and going in circles I looked at the hints given and cannot for the life of me even understand the logic behind the hints given and wondering if someone could explain to the logic.

This is the question as displayed above

next is the two hint, which I am fine with as I did the same

Hint three started to confuse me a little so I went on to hint four which is where I have no clue

hint four

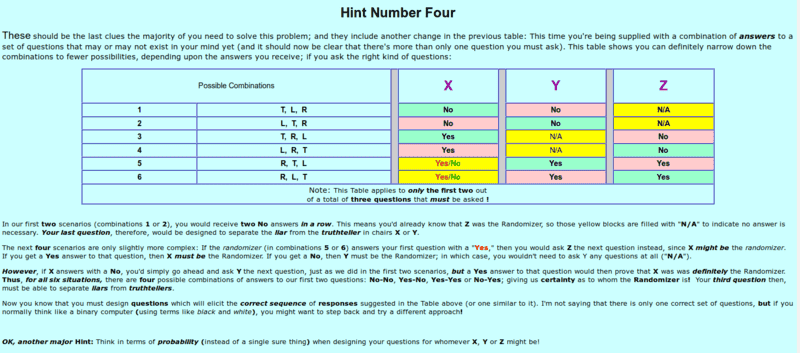
I can't see how by saying 'No' in two rows tells you who the randomize is and by saying yes in 3 and 4 you ask Z next. I just don't understand how this is occurring and wondering if someone could maybe expand on what is happening.

Any advice would be appreciated as I would like to very much improve my skills in logic.

 

[jedishrfu]

Khan Academy has a video on the slightly simpler one of using a single question to find the right door.

https://www.khanacademy.org/math/ma...brain-teasers/v/liar-truthteller-brain-teaser

And here’s the classic scene from the labyrinth movie



Lastly, stack has a discussion on it.

https://puzzling.stackexchange.com/...-lies-one-tells-the-truth-and-one-is-unreliab

 

[PeroK]

Khan Academy has a video on the slightly simpler one of using a single question to find the right door.

But, of course, there is another question:

 

[verty]

Q1 is the key to this puzzle, how to find someone who isn't the randomizer. The rest is easy by comparison, I think.

 

[Taylor_1989]

I understand that you need to find someone whos not the randomize but what bugging me is that in the R1 and R2 he a put No, No, but why can't you put yes, yes

How dose No No show the you know the randomize, and Yes Yes dose not

 

[verty]

I understand that you need to find someone whos not the randomize but what bugging me is that in the R1 and R2 he a put No, No, but why can't you put yes, yes

How dose No No show the you know the randomize, and Yes Yes dose not

I don't think those hints are particularly helpful (I don't understand them myself). Can you solve the simpler, two-door puzzle?

 

[Taylor_1989]

I don't think those hints are particularly helpful (I don't understand them myself). Can you solve the simpler, two-door puzzle?

Yes two door puzzel was not bad, I compared my ans with the above video and was fine. But it the randomizer that confusing me, Iv been looking around at other similar question and people methoda, all of which seem to say if yes 'turth teller or random' if no 'liar' ehich seem to fit the hints above, but I can't see how you can have a question that negates the random.

So ine example i saw for this question was, "ask if he a man" to person A for example and the respones were if yes 'turth teller or random' and if no 'liar'.

But to me that wrong beacuse random could also say no as well. There also some implying you could ask if they are random and the person would not respond, again I don't think correct. Asking that question woukd not filter the random person.

To one attemot i tried was asking A is B always truthful but if you list the 6 possible outcomes of the line up and see A response to each, the truth teller and liar both say no but the random can say either so you stuck in my book beacuse what ever next question you ask the random is still always there.

 

[verty]

Suppose you know that A is not the randomizer. Can you find the randomizer with one question?

 

[Taylor_1989]

Suppose you know that A is not the randomizer. Can you find the randomizer with one question?

I don't think you can, as to me it would depend on the next question, so what I have done is this:

Iv asked A 'Dose B tell more truth than C', this results in the folowing y/n

y : (TRL), (LRT)

n : (TLR), (LTR)

As you can see from the above, you can't narrow done the randomizer, is there a fault with how I am working this out?

Why would you assume that? And if you were to repeat the experiment can you assume B is not the randomizer?

 

[verty]

Here is another question. Suppose I am talking to the liar. How can I get the liar to tell the truth? Do you see it is something like "What would you say if I asked you..."?

Suppose you know that A is not the randomizer. Can you find the randomizer with one question?

Can you answer this now?

I think this is all the help I can give for this question. I hope it helps.

 

[willem2]

If there was no random, you could get a true yes/no answer to any question, no matter who you ask.
If you want to ask a non-random a question Q, they will answer with (I am a liar) xor Q . (xor means: exactly one of those 2 statements is true). Q can be any logical expression you want. It shouldn't be too hard to reverse this process and come up with a question to which the answer is Q. If you do that you get any yes/no question truthfully answered by any non-random.

So it would really help if you knew someone who was not random after the first question. Of course, if you want to know if Person A is random, it won't help to ask Person A.

 

[SSequence]

One interesting thing about the labyrinth video is that when one of the guards initially says along the lines of:
p: one of us always lies and the other always tells the truth ......
then:
If that guard is telling the truth (in the given instance), then he has to be the one that always tells the truth (since the other one "always" lies).

And if he isn't telling the truth, then we have to assume the negation of p. And apparently, the negation should include enough possibilities that it probably(?) becomes impossible to inquire the required truth (with 100% confidence) with just one question (or even arbitrary no. of questions?) ... probably needs to be checked in detail though.

 

[PeroK]

One interesting thing about the labyrinth video is that when one of the guards initially says along the lines of:
p: one of us always lies and the other always tells the truth ......
then:
If that guard is telling the truth (in the given instance), then he has to be the one that always tells the truth (since the other one "always" lies).

It may be a refinement to have the guards only tell the truth or lie in response to the specific question of which door is which. That avoids the liar revealing himself in any other way.

Also, if you can assume that the liar guards the bad door and the truthteller guards the good door, then you can solve the problem via the "treefrog" type question. Having the guards only lie about the doors avoids that issue as well. The other solution to this is not to have the guards assigned to a door, but independent of the doors. That way, identifying the liar by another means doesn't immediately tell you which door is which.

 

[SSequence]

It may be a refinement to have the guards only tell the truth or lie in response to the specific question of which door is which. That avoids the liar revealing himself in any other way.

Also, if you can assume that the liar guards the bad door and the truthteller guards the good door, ...

Yeah, it can be avoided in few ways.

Normally, it is not an issue because we are given this information as a puzzle (in a book or online etc.) ... so we obviously assume it to be true (as assumption of question).

Also for the last sentence ... I think, in that specific case, just asking 2+2=4 should suffice?