BinBinBinBin
- 3
- 0
Hi, I'm working on an independent research project - and am trying to integrate this (with respect to x between some arbitrary m and infinite).
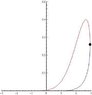
http://www.wolframalpha.com/input/?i=+x+=(t+2)/(1+e^(t-r)),+y=(e^(-t^2/2))/sqrt(2*pi)
If you graph this as a parametric eqn (set r to 2 or 3), the problem is that it is not a one-to-one mapping. I want to find the area under the curve (and the part where there are two values of x, I want to include that twice.
Is there any way I can do this?
In the end I want to have the integral be a function of r (m is constant) that I can use elsewhere.
I want to see how the area under the curve changes when I vary r
Any suggestions?
http://www.wolframalpha.com/input/?i=+x+=(t+2)/(1+e^(t-r)),+y=(e^(-t^2/2))/sqrt(2*pi)
If you graph this as a parametric eqn (set r to 2 or 3), the problem is that it is not a one-to-one mapping. I want to find the area under the curve (and the part where there are two values of x, I want to include that twice.
Is there any way I can do this?
In the end I want to have the integral be a function of r (m is constant) that I can use elsewhere.
I want to see how the area under the curve changes when I vary r
Any suggestions?
Last edited: