Turbine Work - Can I assume ideal gas?

[Sorade]

Hi all,

I need to estimate the mechanical work I can recover from expanding hot air through a gas turbine.

So far I am using the equation below, where Wrev is my ideal isentropic work, s the number of stages, n = k = ratio of specific heats, R gas constant, T1 is the inlet Temperature, Pin the inlet pressure, Pout the outlet pressure.

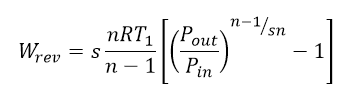
This equation was derived assuming an ideal gas was used. I would like to know how valid this is when the inlet conditions are T = 600 K and P = 250 bars, and outlet conditions T = 350 K and P = 1 bar.

I am asking because I saw this simplification used in many papers and I want to know what impact that might have on my estimations. I assume an isentropic efficiency between 0.66 and 0.88 and calculated all the work outcomes for the values in this range.

 

[Nidum]

Your inlet conditions and overall pressure ratio are not very plausible - is this a real engineering problem ?

 

[MHrtz]

I would imagine the effect of the gas compression would be negligible. Theoretically, air should behave like an ideal gas in this case because it is under high temperatures.

If you want to verify, you could always determine the compressibility factor of air at the inlet condition and outlet condition and apply those to the formula. Then calculate a percentage difference between what you originally calculated vs. what you calculated when accounting for the compressiblity of the gas. You could then determine if the difference is negligible for your application.

 

[Sorade]

Thanks. I suspected it would be okay with high temperatures, but I wasn't sure that the high pressure wouldn't counter act that.

Nidium, I am not sure I used the correct outlet temperature, it is not needed for the equation and I usually work it out separately once I worked out the amount of work to extract. I terms of the pressure ratio being massive, this is because I actually have 2 or 3 stages, represented by s in the equation.

 

[Nidum]

Properties of air over a wide range of pressures and temperatures can be obtained from published data .

Properties of air mixed with combustion products are also available .

You would need a large number of turbine stages to handle that pressure drop . Certainly many more than 2 or 3 .

The number of stages is a bit academic though because such a turbine would be impractical both for thermodynamic reasons and because of practical difficulties of construction .

You can find large amounts of useful information on this subject from books and websites dealing with gas turbine design .

 

[Sorade]

Thank you Nidum,

Apologies if it sounds a bit academic, I'm not a mechanical or electrical engineer, so I had to start from scratch.

Do you have any example of good starting points to look at maximum inlet pressures of gas turbines ? I am looking at a system where the compression of the gas is decoupled in time, so that might remove some of the limitations ?? I basically consider the combustion chamber + expander part of the turbine.

 

[Nidum]

Pressure ratios for land based power generator gas turbines are typically in the range 10:1 to 20:1 . Some advanced technology jet engines have pressure ratios up to 25:1 .

So turbine inlet pressures are in range 10 bar to 25 bar .

For the energy storage and recovery system that you are exploring it would probably be best to use a pressure at the lower end of this range .