Nina87
- 2
- 0
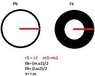
two balls, one made of iron and one made of lead with same radius and mass. which one will roll down the slope faster?
i don't really know where to begin, since everything is the same, the only idea i had was to somehow relate Ek=(J.ω2)/2 => Ek= m.r2.(ω2/2) to the question since i imagine that for them to r1=r2, m1=m2 one must have thinner wall. but then i can't isolate 'v' from the equation to actually prove something.
i don't really know where to begin, since everything is the same, the only idea i had was to somehow relate Ek=(J.ω2)/2 => Ek= m.r2.(ω2/2) to the question since i imagine that for them to r1=r2, m1=m2 one must have thinner wall. but then i can't isolate 'v' from the equation to actually prove something.