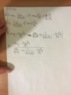- #1
MathError
- 25
- 0
Homework Statement
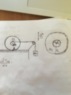
A solid body consisting in two concentric disks of masses m1, m2 and radius r1<r2 is linked through a ideal rope to a mass m which falls down with a certain acceleration. The solid body moves of pure rolling.
Find the acceleration a of the mass.
Homework Equations
P-T=m*a
T-F=(m1+m2)*A
I=1/2*m1*r1^2+1/2*m2*r2^2
T*r1+F*r2=I*alpha
SQ=w*r1+Scm or Sq=w*r1
a=aQ=alpha*r1+A or a=aQ=alpha*r1
A=alpha*r2
The Attempt at a Solution
The mass m is subject to its weight force P=m*g and the tension T of the rope so:
P-T=m*a
T-F=(m1+m2)*a
On the solid body the tension and the grip of the floor (F) act:
T-F=(m1+m2)*A
I chose the center of mass (cm) as the pole of momentum of forces:
T*r1+F*r2=I*alpha
I=1/2*m1*r1^2+1/2*m2*r2^2
now I tried to find a relation between a and alpha: the acceleration and the speed of the piont Q has to be equal to the speed and the acceleration of the mass because the rope can't extend. So SQ=w*r1+Scm and a=aQ=alpha*r1+A (indeed I don't know if SQ=w*r1+Scm or simply SQ=w*r1 in fact, in the solution of the problem I found that SQ=w*(r1+r2) but it has chosen the point P as pole for the momentum on the forces which ita speed is istant by istant naught). Since the body rolls without slither, the acceleration A of the center of mass and alpha must satisfy the condition A=alpha*r2.
I solved the sistem of equations (I tried both the equations for the speed) but in any case my solution was wrong. I hope you can help me.
Thanks a lot