Two equations "combined" don't give the desired result

[nomadreid]

Homework Statement

From only (A) x'=g(x-vt) and (B) x^2-(ct)^2=x'^2-(ct')^2 derive
(C) t'=g(t-(vx/c^2)),

Relevant Equations

g= gamma = 1/sqrt(1-(v/c)^2) and the equations in the Statement

In https://phys.libretexts.org/Bookshe...__Relativity/5.06:_The_Lorentz_Transformation

First, the equation (5.6.7) apparently has a typo: the x' should not be in the denominator, as one can see by comparing it with the equation just above it from which it was derived. The corrected equation is Equation (A) in the Statement (standard Lorentz transformation).

Then two equations down (unnumbered), the author states the equation (B) in the Statement,
"We combine this with Equation 5.6.7 that relates x and x' to obtain the relation between t and t′:"
and then states the equation (C) in the statement.

How he means to "combine" them is what I don't successfully get. I tried substitution of x' from (A) into (B), and got a mess; I then tried solving (B) for x', and substituting this solution into (A), and got the same mess, that is,
(A) into (B)

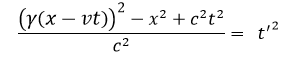
which doesn't simplify to (C). Either: (a) my algebraic manipulation is wrong; (b) the author is including some other equation in the derivation.
Any indications where this is going wrong would be greatly appreciated. (Yes, there are other ways to derive the relation (C), but I am interested in this author's derivation.)

 

[Orodruin]

which doesn't simplify to (C)

Yes it does (up to the sign of the square root).

 

[nomadreid]

Thanks, Orodruin. OK, I will try again, now with the assurance that I just made some minor mistake made in simplifying. That fully answers my question! Super!

 

[nomadreid]

update: found the error. It all comes out. Thanks again, Orodruin