Two movable pulleys lifting a mass

In summary: The diagram shows three separate, inextensible strings attached at intervals of λ around the periphery of the inner disk.
  • #1
rashida564
220
6
Homework Statement
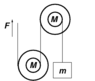
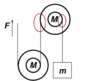
Each pulley is replaced by a system of two concentric disks, which are fastened
together and are free to rotate about a fixed, common axle. Each system has mass
M and moment of inertia MR2/2, and the radius of the inner disk is R/2 and that
of the outer disk is R. Light, inextensible strings of the same material as in part (d)
are wrapped around each disk system, as shown in the diagram below, and the same
block of mass m is to be lifted by the force of magnitude F. Find the maximum
possible acceleration of the block in this case.
Relevant Equations
t=Iα
F=ma
I solved the last part of the previous question, But I got no idea how to start solving this question Like how the rope is being attached, is it attached to the inner disk or the outer one.
 

Attachments

  • pulley 2.PNG
    pulley 2.PNG
    15.6 KB · Views: 288
Physics news on Phys.org
  • #2
Please post your FBD.
 
  • #3
This is the FBD that I think about
 

Attachments

  • pulleys .jpg
    pulleys .jpg
    25.4 KB · Views: 225
  • #4
I think the position of the mass I drawn it wrongly
 
  • #5
I am thinking of solving it this way.
Let the pulley on the left be 1 and the one on the right be 2.
Sign convention
Let counter clock wise be positive and up also be positive.
For first pulley
-FR+T1(R/2)=(MR^2/2) α1
For the second pulley
T1(R)-T2(R/2)=(MR^2/2) α2
Now I now that α1=-α2, and α at any point is a/r. where r is the distance from the rotation axis. if I putted r=R, and a=a3. Then those equation becomes
2F-T1=Ma3 for the first pulley
and 2T1-T2=Ma3
Now for the block
T2-mg=ma3
Putting T1=5Mg, sorry I forgot to mention this in the question "maximum tension on the rope is 5Mg"
Then T2=2T1-Ma3 (Now this is confusing since if M was small small really small, then T2 is approximately equal to T1 which means that it will break" but I will continue and see what going to happen)
so T2= 10Mg-Ma3
Putting this into the block equation.
10Mg-mg=a3(M+m)
so a3= (10Mg-mg)/(M+m)
 
  • #6
rashida564 said:
Now this is confusing since if M was small small really small, then T2 is approximately equal to T1
I don't think so. It's rather worse than that.
 
  • #7
sorry I mean if M was small then it will be twice, so the rope will break. Is it because there's something wrong in the equations
 
Last edited:
  • #8
rashida564 said:
Now I now that α1=-α2
Why? Think about the speed of the rope connecting them.
 
  • #9
Sorry for late reply,Oh I think the speed, the tangential speed of the rope must be the same, and there will be two angular acceleration I think, one of the small radius and the other for the big radius.
 
  • #10
rashida564 said:
Sorry for late reply,Oh I think the speed, the tangential speed of the rope must be the same, and there will be two angular acceleration I think, one of the small radius and the other for the big radius.
Right.
 
  • #11
I am confused about how to describe the equation. should I used to think α is the angular acceleration at the furthest distance from the rotation point "same distance as R in moment of inertia". So I got no idea what does α stand for other than being a rotational acceleration.
 
  • #12
rashida564 said:
I am confused about how to describe the equation. should I used to think α is the angular acceleration at the furthest distance from the rotation point "same distance as R in moment of inertia". So I got no idea what does α stand for other than being a rotational acceleration.
If the rope connecting them is accelerating downward at rate a, what are the two angular accelerations of the pulleys?
 
  • #13
The rope is connected to both of inner and outer and acceleration is the same so for the inner it should be twice the outer radius.
 
  • #14
rashida564 said:
The rope is connected to both of inner and outer and acceleration is the same so for the inner it should be twice the outer radius.
If you mean the angular acceleration of the pulley where the rope is on the inner disc will be twice that of the other pulley, yes.
 
  • #15
Sorry i thought for both of them the rope is on the inner disk, I though it's in the inner rope then goes to the outer rope and connected again to a second pulley by the inner then the outer
 
  • #16
rashida564 said:
Sorry i thought for both of them the rope is on the inner disk, I though it's in the inner rope then goes to the outer rope and connected again to a second pulley by the inner then the outer
I'm really not sure what you are saying there.
The rope that connects the pulleys runs from the outer disc of the upper pulley to the inner disc of the lower pulley. The determines the relationship between the two angular accelerations.
 
  • #17
Sorry I thought each rope is connected to both the inner and the outer
 

Attachments

  • pulley 2.PNG
    pulley 2.PNG
    15.1 KB · Views: 208
  • #18
rashida564 said:
Sorry I thought each rope is connected to both the inner and the outer
There are three separate ropes.
 
  • #19
Sorry but how do we know that they are separate ropes
 
  • #20
rashida564 said:
Sorry but how do we know that they are separate ropes
The diagram shows a rope from the suspended mass rising up to and wrapping around the inner disc of the upper pulley. It does not show that rope going anywhere else, and if it did things would get in a tangle.
It also shows a rope wrapping around the outer disc of the upper pulley and the inner disc of the lower pulley. Again, it is not shown continuing anywhere beyond.

The question says
"Light, inextensible strings of the same material as in part (d) are wrapped around each disk system"
Strings, plural.
 
  • #21
Won't the middle rope for both of them have the same tangential speed, so for each pulley their will be two tangential speed one of each rope
 
  • #22
If the middle rope on the left hand pulley has speed v, what is the speed of the outer rope on the right hand pulley?

Since they are the same rope, this should be an easy question to answer.
 
  • #23
rashida564 said:
Won't the middle rope for both of them have the same tangential speed, so for each pulley their will be two tangential speed one of each rope
Yet again, I am really not sure what you are saying. I am guessing there is a language issue.
If the section of rope connecting them is moving down at acceleration a, what is the angular acceleration of the upper pulley?
 
  • #24
Sorry mate my English is my second language, I need to improve it. I see it now the upper will have half the angular acceleration of the lower, since they are connected by the same rope. From that we can find the tangential acceleration of the block. So if the acceleration of the lower is α then for the upper it's α /2. and the tangential acceleration of the block will be α /2(R/2)=α /4R
 
  • #25
rashida564 said:
Sorry mate my English is my second language, I need to improve it. I see it now the upper will have half the angular acceleration of the lower, since they are connected by the same rope. From that we can find the tangential acceleration of the block. So if the acceleration of the lower is α then for the upper it's α /2. and the tangential acceleration of the block will be α /2(R/2)=α /4R
Yes ( but for clarity I would write αR/4).
 
  • #26
I don't know if this is true physically. I am just thinking of consider the second pulley. The one in the right. I know it will move counter clock wise, so if I putted the counter clockwise as positive direction.
Then I will get that
T1R-T2R/2= MR^2 α/4
4T1-2T2= MR α
But now here's the problem α is positive since I choose this to be the positive direction. and T must be positive.
So T1=5Mg. But now here's the problem that the coefficient of T1 is bigger than T2, I know I am missing a negative sing but I don't know what's the physical reason to make me put the negative sign.
 
  • #27
rashida564 said:
so if I putted the counter clockwise as positive direction.
Then I will get that
T1R-T2R/2= MR^2 α/4
Your T1 is for the rightmost rope, yes? That exerts a clockwise torque, so should be negative.
 
  • #28
I putted T1 as for the left rope 😭😭
 
  • #29
rashida564 said:
I putted T1 as for the left rope 😭😭
Ah. Originally you had T1 as the rightmost of the three and T2 as the central rope. Please switch back to that..
rashida564 said:
So T1=5Mg
No. It wouid be that if the block were not accelerating.
rashida564 said:
here's the problem that the coefficient of T1 is bigger than T2
Why is that a problem?
 

Similar threads

Newton's Second Law (Pulley Sustem)
Replies
3
Views
2K
System of two pulleys and three masses
Replies
22
Views
5K
What mass must be placed on the cord to keep the pulley from rotating?
Replies
1
Views
522
Olympiad dynamics problem with 3 masses and a pulley
Replies
17
Views
2K
Tension Question with One Mass and Two Pulleys
Replies
7
Views
911
Falling mass, additionally accelerated by a rope
Replies
18
Views
839
How does this system work? (Four pulleys and a rope lifting a mass)
Replies
5
Views
1K
Absolute motion analysis of pulley-spring system
Replies
10
Views
727
Block and pulley on movable incline
Replies
2
Views
1K
Mass Pulley and torque -- Confusion in this Atwood machine problem
Replies
11
Views
542

Hot Threads

Recent Insights

Back
Top