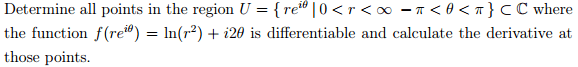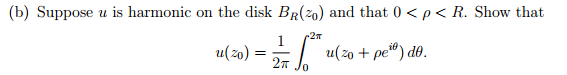nacho-man
- 166
- 0
Could I get some hints on how to evaluate these question.
The question asking to find where $f(re^{i\theta})$ is differentiable doesn't seem to involved,
however would I use C-R equations, or would it just be for wherever $r \neq 0$. Although that is given in the domain, so I'm assuming they want us to use C-R equations.
If i were to use C-R equations, then I would have to convert to cartesian coordinates, correct?
How would I do that.As for the second question,
could I get any hints on what theorems may be relevant. I am not sure how to approach this.
Thanks
The question asking to find where $f(re^{i\theta})$ is differentiable doesn't seem to involved,
however would I use C-R equations, or would it just be for wherever $r \neq 0$. Although that is given in the domain, so I'm assuming they want us to use C-R equations.
If i were to use C-R equations, then I would have to convert to cartesian coordinates, correct?
How would I do that.As for the second question,
could I get any hints on what theorems may be relevant. I am not sure how to approach this.
Thanks