NecroWinter
- 8
- 0
problem: sin(x)^2cos(x)
integrate from 0 to pi/2the way I tried this is by making u = sin, and then working with du to make cos cancel out
the next thing I did was check my new intervals by plugging in pi/2 and 0 into the u function (becomes 0 to 1)
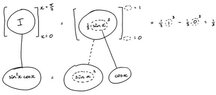
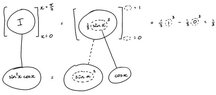
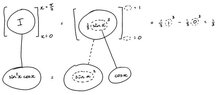
next, I took the anti derivative of u, which came to (u^3)/3((u^3)/3))-((u^3)/3)
sin0=0
sin pi/2 = 1(0^3)/3 - (1^3)/3 = -1/3except, wolfram alpha gives me 1/3.What happened?
integrate from 0 to pi/2the way I tried this is by making u = sin, and then working with du to make cos cancel out
the next thing I did was check my new intervals by plugging in pi/2 and 0 into the u function (becomes 0 to 1)
next, I took the anti derivative of u, which came to (u^3)/3((u^3)/3))-((u^3)/3)
sin0=0
sin pi/2 = 1(0^3)/3 - (1^3)/3 = -1/3except, wolfram alpha gives me 1/3.What happened?