SUMMARY
The discussion centers on the Uncertainty Principle as it relates to angular momentum (L) and angular position. It establishes that the uncertainty in angular momentum is directly related to the uncertainty in angular position, specifically when a particle of mass m moves in a circular path with a fixed radius r and speed v. The participants explore the conditions under which the uncertainty in L leads to a complete indeterminacy in angular position, emphasizing the need for a mathematical approach to validate these relationships.
PREREQUISITES
- Understanding of quantum mechanics principles, specifically the Uncertainty Principle.
- Familiarity with angular momentum concepts in physics.
- Basic knowledge of circular motion and its mathematical representations.
- Ability to manipulate equations involving uncertainties in physical quantities.
NEXT STEPS
- Research the mathematical formulation of the Uncertainty Principle in quantum mechanics.
- Study the implications of angular momentum quantization in quantum systems.
- Explore examples of particles in circular motion and their associated uncertainties.
- Investigate the relationship between position and momentum uncertainties in more complex systems.
USEFUL FOR
Students and professionals in physics, particularly those focusing on quantum mechanics and angular momentum, as well as educators seeking to clarify the Uncertainty Principle's implications in practical scenarios.
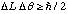, where
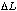is the uncertainty in the angular momentum of a particle, and
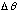is the uncertainty in its angular position. (You may think of a particle, mass m, moving in a circle of fixed radius r, with speed v)