Understanding a Homopolar Generator

[jisbon]

Homework Statement

Give an expression for the induced current in a homopolar generator as a function of angular velocity $\omega$

Relevant Equations

-

So I was searching up on the homopolar generator and found this explanation for the generator, as well as the proposed solution.

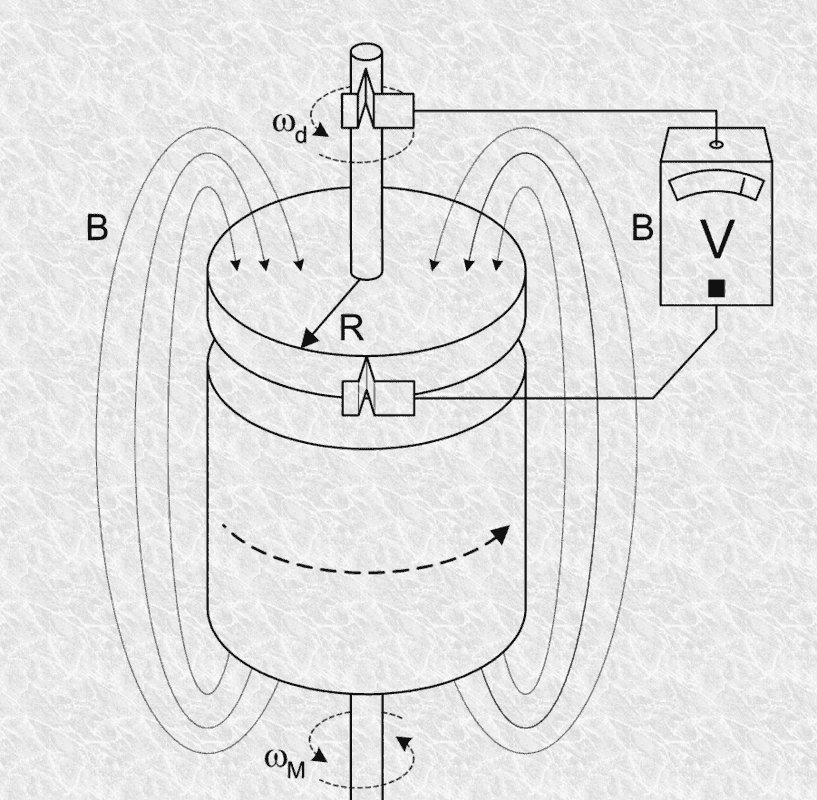
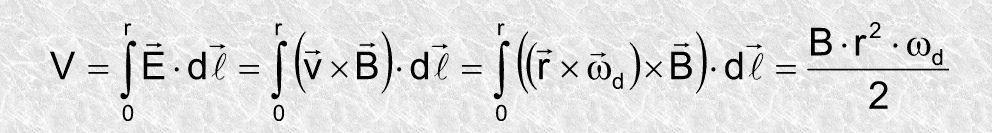
However, I don't really understand what the solution is trying to do here.

Ok, I understand to find the current, you will need the potential, which is the integration of emf. However, I'm stuck at the last part. How did they exactly derive $dl$and what is $dl$ exactly?

Any explanation will be appreciated. Thanks

 

[mitochan]

Hi.
$d\mathbf{l}$ is along the line between shaft and contact point. $d\mathbf{l}$ and emf working on the line have same direction, with plus or minus signature.

 

[Delta2]

I think the integral "overloads" the symbol $r$ as it uses it both at the integral boundary (from 0 to r) and to denote the position vector along the path of integration which is along a radius R. I think it would be more proper to denote the $\vec{r}$ as $\vec{l}$ and then everything falls into place cause then $d\vec{l}$ gains its meaning inside the integral.