- #1
looseleaf
- 24
- 1
I was wondering how to deal with this step in Peskin and Schroeder:
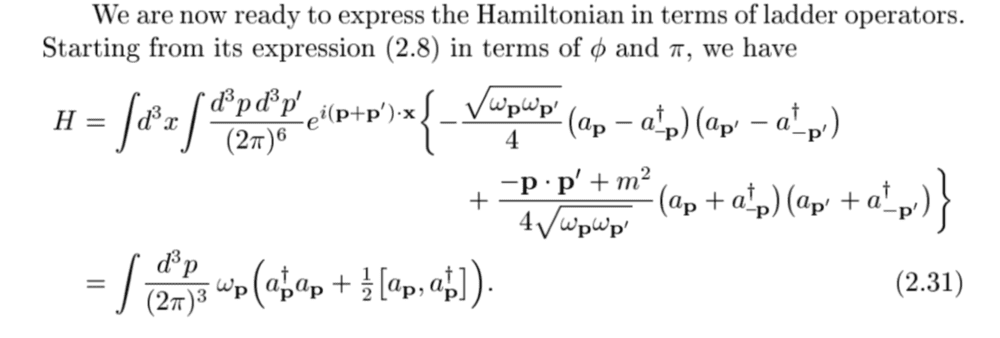
So first you make the delta fn. from the exponential as d(p - (- p')), then what do you do with the creation/annihilation operators that have a negative subscript? I don't have to go into position/momentum representation do I?..
So first you make the delta fn. from the exponential as d(p - (- p')), then what do you do with the creation/annihilation operators that have a negative subscript? I don't have to go into position/momentum representation do I?..
Last edited: