Discussion Overview
The discussion revolves around understanding binary long division, specifically focusing on when a digit in the quotient is zero. Participants are examining an exercise involving binary division and its application, including a potential misunderstanding of the method used.
Discussion Character
- Exploratory, Technical explanation, Debate/contested, Homework-related
Main Points Raised
- One participant questions the reasoning behind the first digit being 1 in the quotient when comparing 1111 and 1010.
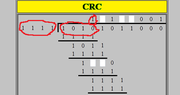
- Another participant presents a visual representation of binary long division, suggesting a standard approach to the division process.
- A third participant speculates that there may have been a mistake in the exercise and expresses intent to identify further errors.
- Another participant clarifies that the division method being discussed is not traditional long division but rather a special type used for computing CRC, noting that the divisor must match the length of the numerator for it to divide correctly.
- This participant also explains that XOR is used instead of subtraction in this method, leading to a zero in the quotient under certain conditions.
- References to external resources are provided for further understanding of CRC and its mathematical background.
Areas of Agreement / Disagreement
Participants express differing views on the nature of the division process, with some adhering to traditional binary long division and others advocating for the CRC method. The discussion remains unresolved regarding the correct interpretation of the exercise.
Contextual Notes
There are limitations in the understanding of the division method being applied, including the specific conditions under which the quotient digits are determined. The distinction between traditional binary long division and CRC computation methods is not fully reconciled.