Why is the derivative of f not linear at the inflection point in concavity?

[22990atinesh]

Hello friends,
I'm trying to understand Concavity, But I've some doubts. As we know quadratic polynomial on graphing forms a parabola opening upwards or downwards. While understanding concavity we divide graphs into separate region using inflection points and each separate region is a quadratic polynomial in its own. So, its derivative should be linear. Then why the derivative of function ' f ' in the domain (vertical green line) is not linear.

 

[jfizzix]

Concavity often has two meanings. First, it is sometimes referred to just as the sign of the second derivative. In the green region, the second derivative is negative, so the function f is "concave down", or we might say the function is concave in that region. In any domain where the second derivative is positive, the function is "concave up", or convex in that region. The concavity also can mean the actual value of the second derivative, so that the quadratic function "a x^2" has a concavity of "2a".

There are also many functions which look like parabolas, but whose real behavior is more complicated, as you see for yourself. Another neat example is the catenary. It is concave up, but its second dervative has different values in different places.

 

[22990atinesh]

Hello jfizzix,
Lets just forget about concavity for a while. the graph of a function f under green vertical lines is a quadratic so its derivative must be linear (a straight line). But as we can see from graph f' its not a straight between green vertical lines.

 

[Mark44]

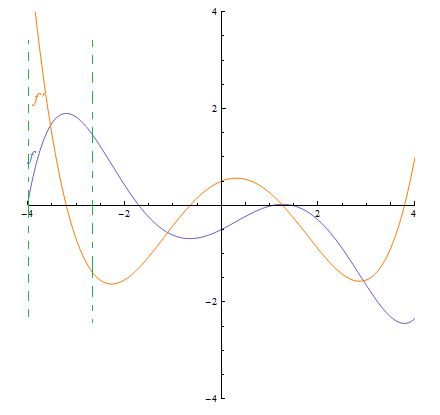
I'm trying to understand Concavity, But I've some doubts. As we know quadratic polynomial on graphing forms a parabola opening upwards or downwards. While understanding concavity we divide graphs into separate region using inflection points and each separate region is a quadratic polynomial in its own.

No.

So, its derivative should be linear.

No.

Then why the derivative of function ' f ' in the domain (vertical green line) is not linear.

Because the separate pieces of your polynomial function (the blue graph) are not quadratic functions. They only appear to be parabolas, but they aren't.

Lets just forget about concavity for a while. the graph of a function f under green vertical lines is a quadratic so its derivative must be linear (a straight line).

You have some misconceptions. The function f appears to be a fourth-degree polynomial, so its derivative is a cubic. On intervals where the graph of f is concave up or concave down, the graph has roughly the same shape as a parabola, but that's where the similarity ends.

But as we can see from graph f' its not a straight between green vertical lines.

 

[jfizzix]

Hello jfizzix,
Lets just forget about concavity for a while. the graph of a function f under green vertical lines is a quadratic so its derivative must be linear (a straight line). But as we can see from graph f' its not a straight between green vertical lines.

If the function f under green vertical lines were a quadratic, than its derivative would be linear. Since the derivative is not linear as you see, the function under green vertical lines is not quadratic.

If it were a quadratic, it would also be symmetric about the peak (at least the in between the lines). You can see that on the right of the peak, the function bends up more than it does on the left the same distance form the peak.

 

[22990atinesh]

No.
No.
Because the separate pieces of your polynomial function (the blue graph) are not quadratic functions. They only appear to be parabolas, but they aren't.You have some misconceptions. The function f appears to be a fourth-degree polynomial, so its derivative is a cubic. On intervals where the graph of f is concave up or concave down, the graph has roughly the same shape as a parabola, but that's where the similarity ends.

Hi Mark44,
You mean every quadratic function is a parabola which is symmetric under the "Axis of Symmetry". If the blue function would have been symmetric then it would have been a quadratic function right.

 

[pwsnafu]

Hi Mark44,
You mean every quadratic function is a parabola which is symmetric under the "Axis of Symmetry". If the blue function would have been symmetric then it would have been a quadratic function right.

$f(x) = x^4$ is symmetric, but not a parabola.

 

[micromass]

Hi Mark44,
You mean every quadratic function is a parabola which is symmetric under the "Axis of Symmetry". If the blue function would have been symmetric then it would have been a quadratic function right.

No, it wouldn't. There are many functions which might "look like" a quadratic function, but which aren't.

For example, take $f(x) = x^4$. This certainly looks like a quadratic function. See https://www.wolframalpha.com/input/?i=f(x)+=+x^4
But it of course isn't a quadratic function.

Another example is the catenary $f(x) = \textrm{cosh}(x)$. See https://www.wolframalpha.com/input/?i=f(x)+=+cosh(x)&dataset=&equal=Submit This can't even be written as a polynomial, let alone a quadratic function.

Finally, you seem to define a "parabola" as any function which looks like this:

This is incorrect. A parabola is the same as a quadratic function. So a function $f$ is a parabola if and only if it has the form $f(x) = ax^2 + bx + c$ for any $x$ (and $a\neq 0$).
So just because it his concave and symmetric and stuff, doesn't mean that it's a parabola.

In particlar, the catenary and the function $f(x) = x^4$ are not parabolas.

 

[22990atinesh]

$f(x) = x^4$ is symmetric, but not a parabola.

pwsnafu Then how can we tell by watching the graph whether it is quadratic or not

 

[micromass]

pwsnafu Then how can we tell by watching the graph whether it is quadratic or not

We can't. If I give you a random graph like

then you can't deduce whether it's a parabola or not. You need more information.

 

[22990atinesh]

We can't. If I give you a random graph like

then you can't deduce whether it's a parabola or not. You need more information.

what information would be suffice to tell by watching the graph it is a parabola.

 

[micromass]

what information would be suffice to tell by watching the graph it is a parabola.

You need to be given the definition of the function (or enough information so that you can derive the function definition).

So if I give you the following graph

then that tells you nothing.

But if I tell you that this is the graph of $f(x) = \textrm{cosh}(x)$, then you can deduce that the above graph is not a parabola since the function $f$ is not quadratic.

On the other hand, if I tell you that this is the graph of $f(x) = x^2 +34$, then you can see that the above graph is a parabola since $f$ is quadratic.

Without the function definition (or enough equivalent information), you don't know anything about the function being a parabola or not.

So in order to prove the function being a parabola, you need the function definition (or similar). But in order to disprove the function being a parabola, you need less. For example, the following function

http://3-ps.googleusercontent.com/x/www.intmath.com/intmstat.com/trigonometric-graphs/328x207xsinx.gif.pagespeed.ic.UxyaheL0qO.png

can never be a parabola, whatever its function definition is. Likewise, if you are given enough input-output pairs, then you can also easily disprove that the function is a parabola.

So disproving something is a parabola is easy, proving it is a parabola is difficult and needs more information.

 

[22990atinesh]

Thanx friends I get it now