SUMMARY
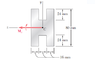
The discussion focuses on calculating the moment of inertia for a beam bending about the Y-axis, specifically for an 80 x 16 mm beam. The correct formula for the moment of inertia is derived as I = (1/12)(80)(16^3) + 80(16)(16^2), with alternative methods discussed, including using the parallel axis theorem (PAT). The final calculated moment of inertia is confirmed as 720,896 mm^4, achieved through both direct calculation and subtraction of cutouts from a larger rectangle. The conversation highlights the importance of understanding the parallel axis theorem in these calculations.
PREREQUISITES
- Understanding of moment of inertia calculations
- Familiarity with the parallel axis theorem (PAT)
- Basic knowledge of beam bending mechanics
- Ability to perform geometric calculations involving rectangles
NEXT STEPS
- Study the application of the parallel axis theorem in structural engineering
- Learn about moment of inertia for various geometric shapes
- Explore advanced beam bending theories and calculations
- Review examples of moment of inertia calculations in engineering textbooks
USEFUL FOR
Engineering students, structural engineers, and anyone involved in mechanical design or analysis of beam structures will benefit from this discussion.