- #1
morpheus343
- 29
- 4
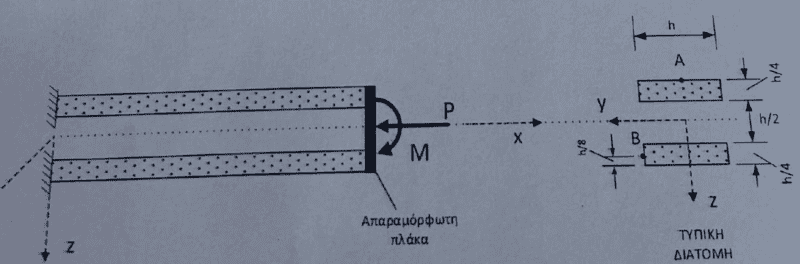
- Homework Statement
- distribution of stress along z, principal stress at point A.
- Relevant Equations
- σA=N/A+-M*y/I
Left side is fixed and right side is held together by a non deformable plate. There are two members with space inbetween. My question is when i want to calculate the stress due to bending moment at point A, which is shown in the crossection, where is the neutral axis? Is it at the middle of the whole thing, where the dotted line is (at the height of the force P), or do i take each member (top and bottom) as individuals and assume the neutral axis at the middle of each beam (h/4*1/2), so the top beam is in tension and the bottom in compression.