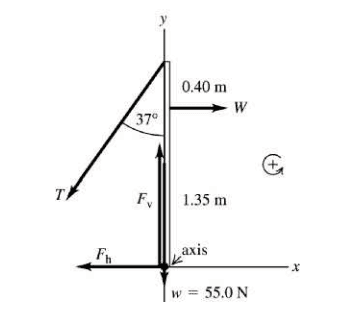
The discussion centers on solving a rigid-body equilibrium problem involving a metal pole and the reaction forces at a pivot. Participants clarify that ##F_h## and ##F_v## represent the horizontal and vertical components of the reaction force exerted by the pivot. The problem can be approached without trigonometry, although some parts may require basic trigonometric understanding, particularly due to the use of a 37-degree angle, which approximates a 3-4-5 triangle. The ambiguity regarding the height of the nail and the direction of the forces is also addressed, highlighting the need for clearer problem statements.
PREREQUISITESStudents and educators in physics, particularly those focusing on mechanics and rigid-body analysis, as well as anyone involved in problem-solving related to equilibrium and forces.
They don't ask for the height of the nail, and don't give enough information to compute it if they did ask, but I still stand corrected.haruspex said:
You’re right, there's not enough information for that, which means I misinterpreted "outward" force. I would have banged the nail in pointing up into the wall, but then the question would would make no sense, so I took it to be horizontal. Outward from the wall is then also horizontal, but then you would need to be able to find the height of the nail.Halc said:
You are welcomeKolika28 said:
