Understanding Solitary Waves: Investigating the Motive Behind Their Formation

  • Context: Graduate 
  • Thread starter Thread starter somasimple
  • Start date Start date
  • Tags Tags
    Wave
Click For Summary

Discussion Overview

The discussion revolves around the formation and characteristics of solitary waves, specifically solitons. Participants explore the mathematical relationships between two snapshots of a soliton at different times and the implications of these relationships for understanding the wave's behavior.

Discussion Character

  • Exploratory
  • Technical explanation
  • Conceptual clarification
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • One participant questions whether the difference between the heights of the wave at two times, fb-fa, can be considered a derivative of the wave function, suggesting it represents the "motive" behind the soliton's formation.
  • Another participant argues that if the wave is moving with a constant speed, fb-fa should equal zero, challenging the notion of a "motive" for the soliton.
  • A different participant describes their approach using discrete values of the wave heights, suggesting that the difference between these values produces a curve resembling a derivative, which can be used to reconstruct the wave shape.
  • There is confusion regarding the subtraction of curves, with one participant seeking clarification on how to interpret fb-fa in this context, proposing a limit that relates to the partial derivative of the wave function.
  • One participant expresses difficulty with mathematical terminology due to language barriers, attempting to clarify their understanding of the relationship between the wave shapes at different times.

Areas of Agreement / Disagreement

Participants exhibit disagreement regarding the interpretation of the difference fb-fa and its implications for understanding solitons. There is no consensus on the meaning of "motive" or how to mathematically represent the relationships discussed.

Contextual Notes

Participants express uncertainty about the mathematical definitions and operations involved, particularly in relation to the subtraction of curves and the concept of derivatives. There are also language barriers affecting clarity in communication.

somasimple
Gold Member
Messages
765
Reaction score
5
Hi,

I'm not really sure the thread fits this forum but I'm not a mathemacian, too. o:)

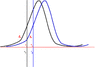
I posted below a picture of a soliton (solitary wave) and I have some questions about it.
We are seeing two snapshots taken at time t1 and t2.
If t2=t1+a with a, small enough?

Can we say that fb-fa equals a kind like of derivative of f (i.e. f')?
can we say that this difference is the motive/reason of the soliton since fa + (fb-fa) = fb?
 

Attachments

  • soliton_0111.gif
    soliton_0111.gif
    10 KB · Views: 487
Physics news on Phys.org
If I understand your picture correctly, fa is the height of the wave at a given time, t1, and position,x1, and fb is the height of the wave at a later time, t2, and positon,x2, such that x1-ct1= x2- ct2; in other words, "moving with the wave". Given that, fb-fa= 0. I have no idea what you might mean by "motive/reason" of a soliton.
 
Hi,

The graph/picture shows two aspects of the same soliton at t1 and t2.
fa is the "curve" at t1 and fb is the curve at t2.

I tried with discrete values (the y values of the curves fa and fb) and I found that substracting fb-fa gives a motive (another curve) that looks like the derivative of fa or fb.
If I add this motive curve values to fa then I obtain fb?
(It seems to work).
 
If fa and fb are curves, then what do you mean by "fb-fa"? I don't know how to subtract curves! Do you mean that fb is a function of x, fb(x)= f(x,b) where f(x,t) is the height of the curve at t= b? In that case, fb- fa= f(x,b)- f(x,a) and then
[tex]lim_{a\rightarrow b}\frac{fb-fa}{b-a}[/tex]
is the partial derivative of f with respect to t.

I still don't know what a "motive curve" is! I suspect you are translating from some language I don't speak.
 
Hi,

Sorry for my poor maths language and unfortunately I'm French that complicates our affair.

We could say that fa and fb are the same shape (motive/reason) of the traveling wave taken at diffrent time t1 and t2.
The shape has of course an equation that I do not know but I have discrete values. With these values I can substract 2 digitized curves that gives a third set of values that looks like the derivative of the equation of the shape?

This third set has also an equation but if I consider only the set I have, I can reproduce fb (shape) simply adding the values of fa with the values I got with my previous computation.

Hope it is a bit clearer?
 

Similar threads

Graduate In light of new evidence, what might be behind the Casimir Effect?
  • · Replies 46 ·
2
Replies
46
Views
6K
Graduate Understanding the Motivation Behind Quantizing Fields in Quantum Field Theory
  • · Replies 98 ·
4
Replies
98
Views
13K
Studying Approaching My 10 Week "Summer" Study Plan
  • · Replies 9 ·
Replies
9
Views
3K
Mathematica This Week's Finds in Mathematical Physics (Week 242)
  • · Replies 1 ·
Replies
1
Views
4K
Mathematica This Week's Finds in Mathematical Physics (Week 248)
  • · Replies 1 ·
Replies
1
Views
4K
Graduate Does Quantum Physics Challenge Our Understanding of Reality?
  • · Replies 14 ·
Replies
14
Views
6K
Graduate Basic Question That Will Eat Your Brains
  • · Replies 9 ·
Replies
9
Views
4K
Mathematica This Week's Finds in Mathematical Physics (Week 228)
  • · Replies 2 ·
Replies
2
Views
3K
Mathematica This Week's Finds in Mathematical Physics (Week 228)
  • · Replies 2 ·
Replies
2
Views
4K
Chapter 10: A Tutorial on Causal Significance
  • · Replies 20 ·
Replies
20
Views
5K