Understanding Special Relativity: Time Dilation and Space Contraction Explained

[blueberrynerd]

Hi! I've just began studying Special Relativity, so I'm naturally having trouble understanding some topics. I just need an opinion on whether my understanding of the topic is right or not.

I've been wondering how time dilation is connected to space contraction. For a relativistic moving frame, space contracts in the direction of motion and at the same time, light travels a greater distance and time accordingly slows down to account for the invariant value of c?

I'm just wondering if my understanding of the topic is correct. I'd really appreciate any input.

 

[BruceW]

That's right. Length contraction and time dilation are given by the more general Lorentz transform equations. These equations have the property that the speed of light is the same as measured by any reference frame

 

[BruceW]

To explain length contraction: let's say we have a ruler that we measure to be 1 meter when stationary, then if we measure its length while it is moving, it will be less than 1 meter.
and for time dilation: If we measure a clock to tick once every minute when stationary, then if we measure it while its moving, it will tick once every minute and a half (for example).

 

[blueberrynerd]

Thanks for the reply! :)

So could you say that time dilation and length contraction go hand-in-hand for a relativistic reference frame?

 

[blueberrynerd]

I also understand how the speed of light accounts for time dilation, but I don't understand how it leads to length contraction.

 

[BruceW]

In what way have you learned about how the speed of light accounts for time dilation?
When I first did relativity, my lecture explained to us a geometrical example, where a combination of time dilation and length contraction led to the speed of light being the same as measured by two different observers.

 

[blueberrynerd]

The way I understood it was that light appears to travel a longer path for an observer in a fixed reference frame and since c has to be constant, time appears to be lengthened as well.

 

[BruceW]

Your terminology isn't quite right, but I think you've got the right idea. At the heart of it all, the speed of light must be the same, so clocks and rulers will go slower/get shorter than if you measured them when they were stationary.
If you only allowed time dilation, and not length contraction, then it would not be possible to have the speed of light the same relative to all observers. This is why length contraction must happen.

 

[blueberrynerd]

Would it be correct to say that length contraction causes c to be constant while time dilation happens as a consequence of the invariance of c?

 

[bobc2]

Would it be correct to say that length contraction causes c to be constant while time dilation happens as a consequence of the invariance of c?

Blueberrynerd, I don't know if the space-time sketches will just make things more confusing or not, but some people find it easier to resolve a question like this by visualizing the relationships between different observers and between observers and objects in 4 dimensions. If you think of the four dimensions as X1, X2, X3, and X4, then you can suppress X2 and X3 in the diagrams so as to focus on how things relate in the X1-X4 coordinates. Here are some basic examples.

Looked at in this way you might think more about the consequence of a very mysterious and fundamental aspect of the relativistic 4-D space. If an observer is in motion with respect to a rest system, his X4 axis is rotated. Further, his X1 axis is rotated also such that a 4-D photon world line will always bisect the angle between the X4 and X1 axis. All observers move along their own X4 axis (their world line) at the speed of light. And since the photon world line is always at a 45 degree angle and bisects X4 and X1 for all observers (no matter their speed), then all observers will measure a ratio of 1:1 between the photon's distance traveled along X4 and distance traveled along X1. And of course the speed of light results from our convention for calibrating time along X4 (remember all observers move along X4 at light speed--although what aspect of the observer is actually doing the moving is a very protacted philosophical discussion not appropriate here).

So, I wouldn't put the cause for the relativistic phenomena squarely on the speed of light. It's more a consequence of the strange rotating of all observer's X4 and X1 axes. You see right away in the pictures below that different observers have different 3-D cross-section views of the 4-dimensional universe. The different geometric views result in different observations of times and distances when observing other observers in relativistic motion. I'm just trying to make the point that it is fruitful to study relativity in the context of geometry: 4-dimensions and 3-D cross-section views. You can google space-time diagrams to dig into this in much more detail.

 

[ghwellsjr]

Hi! I've just began studying Special Relativity, so I'm naturally having trouble understanding some topics. I just need an opinion on whether my understanding of the topic is right or not.

You are showing indications of not understanding Special Relativity. Look at these three comments of yours concerning frames:

For a relativistic moving frame, space contracts in the direction of motion and at the same time, light travels a greater distance and time accordingly slows down to account for the invariant value of c?

So could you say that time dilation and length contraction go hand-in-hand for a relativistic reference frame?

The way I understood it was that light appears to travel a longer path for an observer in a fixed reference frame and since c has to be constant, time appears to be lengthened as well.

You need to understand several things about reference frames in Special Relativity.

First off, you should think in terms of a single, stationary reference frame which we use to define the positions of observers and objects as a function of time. Observers and objects can be moving (or stationary), but not the frame. If an observer/object is stationary with respect to the reference frame, then its clocks tick at a normal rate and its rulers are all a normal length, no matter their orientations. If an observer/object is moving with respect to the reference frame, then its clocks tick at a slower rate (with a longer time interval) and its rulers are shortened along the direction of motion.

The speed of light is defined to be c in this single, stationary reference frame. It's fairly obvious that a stationary observer/object would be able to measure the speed of light to be c because its rulers and clocks are normal.

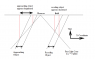
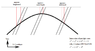
However, you need to know that in order to measure the speed of light, an observer can only measure the round trip speed of light. He needs to have a timing device located at the source of a flash of light and a mirrror some fixed distance away. He starts his timer when the flash is emitted and stops it when he sees the reflected light arrive back at his location. Then to calculate the speed of light, he takes double the distance divided by the time interval.

A moving observer will carry with him a moving light source, a moving timing device, and a moving mirror. Everything moves with respect to him so that for him, everything is stationary.

If he places his mirror in a direction that is at right angles to his direction of motion, then it will take longer for the light to leave the source, travel to the mirror, and reflect back to him. In this case, if his mirror is the same distance away as for the stationary observer, then all it takes is for his timing device to take a longer time per tick so that his measurement will come out the same as for the stationary observer. However, the stationary observer will observe him as taking longer than his own measurement.

If he places his mirror in a direction that is along his direction of motion, then it will also take longer for the light to leave the source, travel to the mirror, and reflect back to him, but if the distance to his mirror is the same as for the previous case, it will take even longer and he will not get the correct answer. For this reason, the distance has to be shortened by just the right amount so that he calculates c for the measured speed of light.

Now, it should also be understood that observers do not have to diliberately move their mirror closer or adjust the tick rate of their clock longer in order for them to measure the speed of light to be c, it happens automatically.

 

[BruceW]

Would it be correct to say that length contraction causes c to be constant while time dilation happens as a consequence of the invariance of c?

If we assume the invariance of c and the principle of relativity are correct, then: length contraction and time dilation must both be allowed. (So they are both a consequence of the invariance of c).
You could say it the other way round, and say that time dilation and length contraction can be used in special relativity to keep c the same as measured by all observers.

Edit: To make it clear, time and space are put on equal footing in relativity. The reason the lengths contract and time dilates is simply because of the way we define the 'proper length' and 'proper time'.

 

[JDoolin]

Hi! I've just began studying Special Relativity, so I'm naturally having trouble understanding some topics. I just need an opinion on whether my understanding of the topic is right or not.

I've been wondering how time dilation is connected to space contraction. For a relativistic moving frame, space contracts in the direction of motion and at the same time, light travels a greater distance and time accordingly slows down to account for the invariant value of c?

I'm just wondering if my understanding of the topic is correct. I'd really appreciate any input.

I'd say you are missing the vital third issue commonly known as the "relativity of simultaneity"

Imagine that you have an open-ceiling circular room ,filled with smoke (to reveal where a flash of light is), and walled with mirrors (to reflect the flash of light), and there is a bright flash of light that emits from the center, passes through the smoke in an expanding circle, bounces off walls (simultaneously), and arrives again simultaneously at the center.

From the point of view of someone hovering directly above the room, it appears that the light hits every part of the mirror simultaneously. However, to someone traveling past at 30% of the speed of light, it should appear as in the animation below.

There are three main differences from the hovering viewpoint and the .3c viewpoint:
(1) The light takes longer to make its outbound and return trip. (time dilation)
(2) The room no longer appears to be circular but slightly oval. (length contraction)
(3) The lignt no longer reaches all parts of the outer circle simultaneously, but instead hits the back end first. (relativity of simultaneity.)

 

[ghwellsjr]

JDoolin, your animation is fantastic. I wish I knew how to create such animations directly on a webpage. The only way I have known to do aminations is to capture them on youtube and point to them indirectly.

Your animation successfully illustrates the point you are making with regard to the relativity of simultaneity.

However, you should state that the views are not those of a person residing within the scenario but are rather for us outside the scenario as we observe what happens according to a defined FoR in which we do not have to worry about how long the image of an event that happens in the scenario takes to reach our eyes outside the scenario.

It's kind of like when we watch ripples on the surface of the water that travel at a very slow speed compared to the speed of light. If we were blind and had to rely on waiting until the water waves reflect off of objects and propagate back to us, we would then be in the same situation as a person in your scenario who won't be able to see the animation as you presented it.

Once you understand that, you will see that you don't need smoke in the room to reveal where the flash of light is because we know where it is based on our defined FoR in which we define the speed of light to be c. In fact, if you think about all the propagations of light within a smoke filled room, you will see that it just presents a lot of confusion because all the smoke lights up with reflections continuing to go in all directions. Nobody could actually see the scenario as you presented it.

But, like I say, take away the smoke and change the perspective from someone in the scenario to us outside the scenario who can observe instantly what is going on at each location within the scenario and you will have a great explanation to go with your great animation.

 

[JDoolin]

JDoolin, your animation is fantastic. I wish I knew how to create such animations directly on a webpage. The only way I have known to do aminations is to capture them on youtube and point to them indirectly.

Your animation successfully illustrates the point you are making with regard to the relativity of simultaneity.

However, you should state that the views are not those of a person residing within the scenario but are rather for us outside the scenario as we observe what happens according to a defined FoR in which we do not have to worry about how long the image of an event that happens in the scenario takes to reach our eyes outside the scenario.

It's kind of like when we watch ripples on the surface of the water that travel at a very slow speed compared to the speed of light. If we were blind and had to rely on waiting until the water waves reflect off of objects and propagate back to us, we would then be in the same situation as a person in your scenario who won't be able to see the animation as you presented it.

Once you understand that, you will see that you don't need smoke in the room to reveal where the flash of light is because we know where it is based on our defined FoR in which we define the speed of light to be c. In fact, if you think about all the propagations of light within a smoke filled room, you will see that it just presents a lot of confusion because all the smoke lights up with reflections continuing to go in all directions. Nobody could actually see the scenario as you presented it.

But, like I say, take away the smoke and change the perspective from someone in the scenario to us outside the scenario who can observe instantly what is going on at each location within the scenario and you will have a great explanation to go with your great animation.

Thank you very much. I made this animation about 10 years ago, I think, using gwbasic. I've long since forgotten how. There is a MUCH easier method now, if you have access to Mathematica:

http://academic2.american.edu/~jpnolan/Misc/MathematicaAnimation.html
Simply Export a Table of Graphics objects into a gif file.

And you're right. In the smoke example, "What you see" is not necessarily what you see in the animation. In fact, as the object is approaching from your left, it would appear elongated, and as it recedes to the right, it would appear even more contracted.

I suspect that if you are looking straight at it, though, as its path-of-motion crosses your line-of-sight at a 90° angle, a little small-angle-approximation could yield a proof that what you would see is at least "approximately" what is shown in the animation. The main concern is whether the speed of light delay is significantly different on the edges of the animation than in the center of the animation. If the object is passing at a distance far enough away, the difference between the path lengths is not significant, so the light from simultaneous events in that region would arrive (almost) simultaneously.


(P.S. Maybe we should want to eliminate the smoke and mirrors anyway, since "Smoke and mirrors is a metaphor for a deceptive, fraudulent or insubstantial explanation or description" http://en.wikipedia.org/wiki/Smoke_and_mirrors :rofl:)

 

[ghwellsjr]

I suspect that if you are looking straight at it, though, as its path-of-motion crosses your line-of-sight at a 90° angle, a little small-angle-approximation could yield a proof that what you would see is at least "approximately" what is shown in the animation. (Edit: But since I neither offer nor link to such a proof, of course, you may doubt that such proof exists. I'm not sure I've ever actually seen such a proof, but I would be surprised if I were wrong.)

Yes, I doubt that a proof exists because it's not correct. The only way you could "solve" this problem is to have a whole bunch of observers above the scenario all spread out so that none of them has to do a small-angle-approximation and they each see delayed in time what is happening below them, but then you have the exact same problem of defining the time delays between them as you would for the observers in the scenario.

Just say that it is we as super observers outside the scenario who can "see" what is going on at any particular location inside the scenario in the "real time" of your FoR and the problem is solved.

 

[ghwellsjr]

(Edit: Maybe we should want to eliminate the smoke and mirrors anyway, since "Smoke and mirrors is a metaphor for a deceptive, fraudulent or insubstantial explanation or description" http://en.wikipedia.org/wiki/Smoke_and_mirrors :rofl:)

Get rid of the smoke but you need the mirrors. You could place partial rings of mirrors of different diameters to let the observer in the center "observe" the progress of the light, but the main point is illustrating how both a stationary observer and a moving observer in any FoR both see themselves in the center of their set of mirrors.

 

[JDoolin]

In fact, if you think about all the propagations of light within a smoke filled room, you will see that it just presents a lot of confusion because all the smoke lights up with reflections continuing to go in all directions. Nobody could actually see the scenario as you presented it.

I'm not entirely sure I agree here. Do a google image search for spotlight smoke or light beam. The apparent location of the light doesn't really stray significantly outside the original region, which is controlled by the shape of the lens of the spotlight. There may be a few rare secondary reflections that would hit your eye, but very few, and far fewer still tertiary reflections.

 

[JDoolin]

Get rid of the smoke but you need the mirrors. You could place partial rings of mirrors of different diameters to let the observer in the center "observe" the progress of the light, but the main point is illustrating how both a stationary observer and a moving observer in any FoR both see themselves in the center of their set of mirrors.

Okay. Putting your observer "at the center" of the room would certainly ruin the "small-angle-approximation" that I was talking about before. My idea is to put both obserers (both the comoving observer, and the observer at .3c) far, far above the room.

You're right, that if you filled the room with smoke, and had the observer inside the room, imagining what that observer "sees" is going to be kind of tricky.

Yes, I doubt that a proof exists because it's not correct. The only way you could "solve" this problem is to have a whole bunch of observers above the scenario all spread out so that none of them has to do a small-angle-approximation and they each see delayed in time what is happening below them, but then you have the exact same problem of defining the time delays between them as you would for the observers in the scenario.

Just say that it is we as super observers outside the scenario who can "see" what is going on at any particular location inside the scenario in the "real time" of your FoR and the problem is solved.

Whoops, I edited my edit already, and then realized you had already replied. Sorry about that. I took out the part where I said "I didn't produce a proof", and put in:

The main concern is whether the speed of light delay is significantly different on the edges of the animation than in the center of the animation. If the object is passing at a distance far enough away, the difference between the path lengths is not significant, so the light from simultaneous events in that region would arrive (almost) simultaneously.​

It's may not pass for a formal proof, but it's pretty strong reasoning.

you have the exact same problem of defining the time delays between them as you would for the observers in the scenario.

I don't see any problem in defining the time delays. It's proportional to the distance from the events to the observer. So IF the distance to the events is approximately the same (as it would be if the observers were far above the room), THEN the time delay is the same, and the events which were simultaneous would appear approximately simultaneous... just delayed.

 

[BruceW]

The time delay due to transmission of speed of light is a problem in a lot of thought experiments.
Often in textbooks, they have to say 'measurements relative to a certain frame, when taking into consideration the delay due to transmission of light'.

 

[ghwellsjr]

Just because you are far away doesn't mean time delays become insignificant. It just means it's harder to actually see the image. You'd have to magnify it tremendously and it's those delays that carry the information to resolve the angles of the light from the different locations far below so that you can actually see what's going on.

Think about it a different way: Until you establish a timing convention, it's impossible to know the one-way speed of light which is necessary in order to build an image of where light is at any given moment. You're not going to trick nature into revealing this information to you by backing far away from the scenario.

That's why I say your animation is an excellent demonstration of what light does according to the timing convention established by Special Relativity for a particular Frame of Reference.

 

[ghwellsjr]

I'm not entirely sure I agree here. Do a google image search for spotlight smoke or light beam. The apparent location of the light doesn't really stray significantly outside the original region, which is controlled by the shape of the lens of the spotlight. There may be a few rare secondary reflections that would hit your eye, but very few, and far fewer still tertiary reflections.

You must have some magic smoke that doesn't attenuate the primary signal significantly but still provides a secondary reflection scattered in all directions but still bright enough to be detected far, far away. Comparison to a spotlight that's on all the time is not really the same. Imagine a flash bulb going off and you're far enough away from it that you can actually see the propagation of the flash through smoke. If the smoke scatters the light enough so that you can see it, it won't last long enough for you to see it hit the mirrors far enough away and reflect back to the origin.

Like I said, if you want to follow the progress, put in small mirrors at measured known distances, or just repeat the entire experiment with progressively larger circular rooms.

 

[JDoolin]

Think about it a different way: Until you establish a timing convention, it's impossible to know the one-way speed of light which is necessary in order to build an image of where light is at any given moment. You're not going to trick nature into revealing this information to you by backing far away from the scenario.

I was under the working assumption that the one-way speed of light is the same as the two-way speed of light; i.e.299 792 458 m/s. If an event happens at a point r away from you at time t, then you wll see that event at time T=t + r/c. Is that what you mean by a timing convention?

P.S. I'll see if I can put together a diagram here in a few minutes, and get a couple of calculations. Maybe I'll proof myself wrong.

PPS. I don't think I proved myself wrong, although I do see there is some interplay with the distance and the angle involved. If you have three simultaneous events (according to the observer) as pictured in the attached diagram, the time delay for the central event is

$${Central Delay} = \frac{d}{c }$$

But the time delay for the events on either side are

$${Edge Delay} = \frac{d}{c \cdot \cos(\theta)}$$

The difference in the delays, then would be $${Difference} = \frac{d}{c }\left ( 1-\frac{1}{\cos(\theta)} \right )$$

So using, for instance d=1000 meters, θ=8°, you would have a field of view (2 d tan(θ)) 280 meters across with simultaneous events appearing no more than 30 nanoseconds apart. This is quite fast compared to the time it take light to travel across the field of view, ≈900 nanoseconds.

You can set the parameters of the thought experiment however you like. (how far away the observers are from the apparatus.) and choose the angle and distance so that (d/c)(1-1/cos(θ) is small relative to the time-scale of whatever phenomena you wish to measure.) (how long it takes light to travel across the circle).

 

[JDoolin]

You must have some magic smoke that doesn't attenuate the primary signal significantly but still provides a secondary reflection scattered in all directions but still bright enough to be detected far, far away. Comparison to a spotlight that's on all the time is not really the same. Imagine a flash bulb going off and you're far enough away from it that you can actually see the propagation of the flash through smoke. If the smoke scatters the light enough so that you can see it, it won't last long enough for you to see it hit the mirrors far enough away and reflect back to the origin.

Like I said, if you want to follow the progress, put in small mirrors at measured known distances, or just repeat the entire experiment with progressively larger circular rooms.

Okay. Putting in small mirrors at measured known distances, so they would reflect a porion of the light out to the observers, would work. Alternatively, we could invoke the "pragmatism immunity" common to all thought experiments, and say for this thought experiment, we use a "smoke that doesn't attenuate the primary signal significantly but still provides a secondary reflection scattered in all directions but still bright enough to be detected far, far away."

 

[ghwellsjr]

I was under the working assumption that the one-way speed of light is the same as the two-way speed of light; i.e.299 792 458 m/s. If an event happens at a point r away from you at time t, then you wll see that event at time T=t + r/c. Is that what you mean by a timing convention?

Yes, that's Einstein's timing convention and once you do that for your diagram, you have specified a Frame of Reference.

P.S. I'll see if I can put together a diagram here in a few minutes, and get a couple of calculations. Maybe I'll proof myself wrong.

PPS. I don't think I proved myself wrong, although I do see there is some interplay with the distance and the angle involved. If you have three simultaneous events (according to the observer) as pictured in the attached diagram, the time delay for the central event is

$${Central Delay} = \frac{d}{c }$$

But the time delay for the events on either side are

$${Edge Delay} = \frac{d}{c \cdot \cos(\theta)}$$

The difference in the delays, then would be $${Difference} = \frac{d}{c }\left ( 1-\frac{1}{\cos(\theta)} \right )$$

So using, for instance d=1000 meters, θ=8°, you would have a field of view (2 d tan(θ)) 280 meters across with simultaneous events appearing no more than 30 nanoseconds apart. This is quite fast compared to the time it take light to travel across the field of view, ≈900 nanoseconds.

You can set the parameters of the thought experiment however you like. (how far away the observers are from the apparatus.) and choose the angle and distance so that (d/c)(1-1/cos(θ) is small relative to the time-scale of whatever phenomena you wish to measure.) (how long it takes light to travel across the circle).

So far, you are analyzing what a stationary observer sees of the stationary scenario below him. It's enough to point out that everything is symmetrical and therefore everything that the observer will see will look like circles.

But now you need to do this for the scenario for which you provided your animation, that is, of a moving observer. Your animation continues for four cycles of light expanding and collapsing and every one of them is identical. You could have continued this on forever, correct? But do you think the observer will continue to see the same thing forever? Isn't it obvious that eventually the angles for viewing each cycle will distort the image so that it doesn't match your animation? Once you see that, you can also see that there is distortion within each cycle right down to the very first one. That's all I'm trying to point out.

But again, just explain your animation as what a FoR defines for what happens without regard to delays caused by light propagation and you will have an accurate descriprtion for your great animation.

 

[ZealScience]

I think relativity implies that space and time cannot be separated. Change in space measurements affects time measurements. So I think that time dilation along with length contraction is intrinsic. I think in the 1916 paper on relativity, there was a derivation of the equations using space time one-to-one correspondence.

 

[BruceW]

That's sort of right. The Lorentz transforms essentially say that length and time measurements in one reference frame depend linearly on length and time measurements in another frame. So we can think of length and time as two axis, and changing to a different reference frame is like rotating this axis.
Time dilation is a special case of the Lorentz transform, where one of the reference frames measures zero spatial separation between two events.
And length contraction is a special case where one of the frames measures zero time difference between two events.

 

[JDoolin]

But do you think the observer will continue to see the same thing forever? Isn't it obvious that eventually the angles for viewing each cycle will distort the image so that it doesn't match your animation? Once you see that, you can also see that there is distortion within each cycle right down to the very first one. That's all I'm trying to point out.

No, the observer won't see the same thing forever. Yes, eventually the angles for viewing each cycle will distort the image. All I'm trying to say is that there is a region where the image is basically not distorted.

I realized this morning, that in order to explain where the image is not distorted, I have to first describe the nature of the distortion we expect, and then point out the region where the distortion is negligible.

The main axiom I'm using here is that the current apparent position of an object according to an observer, is the positional component (in the observer's current rest frame) of the intersection of the objects world-line (or curve) with the observer's current past light cone.

So the attached diagrams show first, a one-dimensional object passing in the y=0 plane. In this plane, the distortion is always present. In the second diagram, a one-dimensional object is passing in the y=d plane. In the y=d plane, there is a small region where there is no significant distortion between the "actual" length-contracted shape, and the "apparent" shape.

 

[ghwellsjr]

We both agree the distortion is at its minimum when the observer is directly overhead but it never goes away, even if you prefer to call it negligible.

But I don't recall you ever agreeing with me that there is zero distortion if you describe the animation as depicting what happens in the plane of the objects according to the observer's rest frame at all times in the past, present and future, and it doesn't matter how high the observer is above the objects. Agreed?

 

[JDoolin]

We both agree the distortion is at its minimum when the observer is directly overhead but it never goes away, even if you prefer to call it negligible.

Good. My main point is that Lorentz contraction and the relativity of simultaneity are things that a person could, at least in principle, observe directly.

But I don't recall you ever agreeing with me that there is zero distortion if you describe the animation as depicting what happens in the plane of the objects according to the observer's rest frame at all times in the past, present and future, and it doesn't matter how high the observer is above the objects. Agreed?

Yes, I agree, and I never meant to disagree on that point. But with one caveat:

(1) assuming that the events in the animation have been happening forever into the past, and into the future. The observer can only reconstruct events as they happened within his past light-cone.

However, I don't think this discussion can be put to rest just yet, because I recalled the reason I am chasing after this point so persistently. Because of a http://www.guspepper.net/electro/Segundo semestre/Seminarios/Funez.pdf" which determined that "the conformality of aberration ensures that, at least over small solid angles, each [co-located observer, regardless of relative speed] will see precisely what the other sees. No Lorentz contractions wll be visible, and all objects will appear normal."

 

[JDoolin]

However, I don't think this discussion can be put to rest just yet, because I recalled the reason I am chasing after this point so persistently. Because of a http://www.guspepper.net/electro/Segundo semestre/Seminarios/Funez.pdf" which determined that "the conformality of aberration ensures that, at least over small solid angles, each [co-located observer, regardless of relative speed] will see precisely what the other sees. No Lorentz contractions wll be visible, and all objects will appear normal."

It appears to me that Terrell is specifying an angle

$$\theta' = \cos^{-1}(v/c)$$

and perhaps at that particular angle, for an approaching object, the Lorentz contraction and the lengthening effect due to the time-delay cancel out. But in general, except for that one special case, I would expect the appearance of the object is distorted the entire time.

 

[ghwellsjr]

Yes, I agree, and I never meant to disagree on that point. But with one caveat:

(1) assuming that the events in the animation have been happening forever into the past, and into the future. The observer can only reconstruct events as they happened within his past light-cone.

I don't know why you think any restrictions are necessary. I only mentioned an observer because I wanted to provide continuity with your earlier description but we don't need an observer so let's just eliminate him. We are not concerned with any observer trying to reconstruct what happened in his past. We are just doing this from the definition of a Frame of Reference.

Let's first consider a Frame of Reference in which the scenario you described earlier is stationary (but without the smoke):

Imagine that you have an open-ceiling circular room ,filled with smoke (to reveal where a flash of light is), and walled with mirrors (to reflect the flash of light), and there is a bright flash of light that emits from the center, passes through the smoke in an expanding circle, bounces off walls (simultaneously), and arrives again simultaneously at the center.

If you had made an animation of this scenario, it would be just as you described it, an expanding circle of light simultaneously hitting all parts of the mirrored wall and collapsing back to the origin, repeating forever.

Now let's consider a new FoR that is moving at 0.3c with respect to the first FoR. Again, there is no observer in the scenario, just a light source and a circular wall of mirrors. Now your animation show exactly what is happening in this new FoR. Don't you agree?

 

[ghwellsjr]

The next thing I was going to have you consider, going back to your far away observers watching the scanario, is what would be the difference between your first observer "hovering directly above the room" and your second observer "traveling past at 30% of the speed of light". From far away, while the second observer is approximately directly above the room, can't you also say that his distortions will be negligible so that he sees approximately the same image that the stationary observer sees?

 

[JDoolin]

The next thing I was going to have you consider, going back to your far away observers watching the scanario, is what would be the difference between your first observer "hovering directly above the room" and your second observer "traveling past at 30% of the speed of light". From far away, while the second observer is approximately directly above the room, can't you also say that his distortions will be negligible so that he sees approximately the same image that the stationary observer sees?

The distortion would be a Lorentz contraction by a factor of $$\sqrt{1-\left(\frac{v}{c}\right)^2}=\sqrt{1-.3^2}=.954$$ compared to what the stationary observer sees.

Whether or not this is negligible is an opinion question, but I've been thinking of 1% difference as a cutoff for negligible. (which is why I used 8 degrees earlier in my calculation).

This would be a 4.6% difference which is above my cutoff, so I would say it is a significant (noticeable) difference from what the stationary observer would see. However, if you asked me to draw a circle free-hand, I imagine I would draw a circle which was even more distorted than 4.6%.

 

[ghwellsjr]

Now consider a stationary far away observer watching the room moving at 30% the speed of light. What would he see?