I Understanding the diagonal elements of the transition dipole moment

[approx12]

TL;DR

How am I supposed to interpret the diagonal elements of the transition dipole matrix. We learned that the matrix elements $\neq 0$ tells us that a certain transition is possible but what if that matrix element is on the diagonal of my matrix. A transition from $|2\rangle$ to $|2\rangle$ for example doesn't make much sense to me.

Hey guys, I just numerically calculated the matrix elements for a superconducting qubit and I'm having some trouble to interpret the result.
I will include a plot of the matrix I got below:

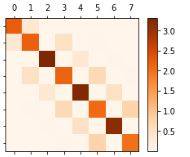
I basically have "large" non zero elements on the main diagonal of this matrix. In previous courses I was told that for example the matrix element $\langle 2|d|3\rangle$ would indicate me that transitions for this quantum system from $2$ to $3$ and vice versa are allowed. Therefore I have a little bit of a hard time understanding the non zero values on the main diagonal.

One interpretation I have is that the system can therefore be polarized but I'm not quite sure about that.

Would be really awesome if someone could share his opinion on this, thank you!

 

[vanhees71]

The transition matrix can always have non-zero diagonal elements. There is some probability that no transition occurs, and that's reflected by the diagonal elements.