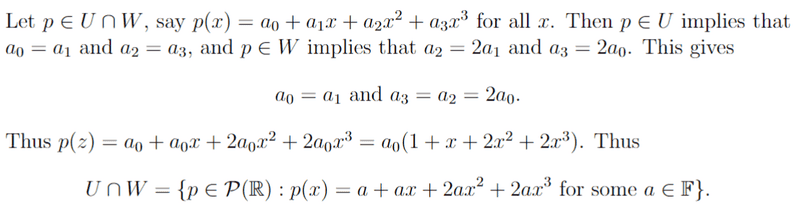SUMMARY
The discussion centers on solving a subspace problem in linear algebra, specifically involving polynomial expressions. Participants confirm that the solution for part (a) is consistent with the equations presented, where the coefficients are defined as ##a_3 = 2a_1## and ##a_2 = 2a_0##. There is a consensus that a typographical error exists in the original problem statement, where ##p(z)## should be corrected to ##p(x)##. The final conclusion indicates that the intersection of subspaces U and W is represented as ##U \cap W = \{a(1+x+2x^2+2x^3)\,|\,a\in \mathbb{F}\}.
PREREQUISITES
- Understanding of linear algebra concepts, specifically subspaces.
- Familiarity with polynomial expressions and their coefficients.
- Knowledge of notation used in linear algebra, such as ##\mathbb{F}## and ##\lambda##.
- Ability to interpret and manipulate equations involving variables and coefficients.
NEXT STEPS
- Study the properties of subspaces in linear algebra.
- Learn about polynomial functions and their coefficients in detail.
- Explore common typographical errors in mathematical texts and their implications.
- Investigate the use of notation in linear algebra to avoid confusion in problem-solving.
USEFUL FOR
Students and educators in mathematics, particularly those focusing on linear algebra, as well as anyone involved in solving polynomial equations and understanding subspace intersections.