belliott4488 said:
I'm not sure what you mean by "radial." You've got two space-time points, and you construct the vector between them, i.e. the space-time interval. It has both time and space components, of course, and only in Bob's frame is it purely spatial, i.e. the time component is zero. But I don't see how that make it a "radius" of anything in particular.
Let's say, for sake of argument, I displace Rachel by one unit space within Bob's frame. Does Rachel's velocity in Bob's frame change, or is it still \frac{\delta s(t)}{\delta t} at any given time? I assume you will agree that spatial displacement of Rachel within Bob's frame has no effect on Rachel's velocity in Bob's frame.
If we map the above into Rachel's frame, Bob is now offset by some space-time interval that is equivalent to one unit space within Bob's frame. It is not clear to me how Rachel can determine whether the time component of that interval is positive or negative without making some additional determination: Is Bob approaching, or receding (radially)? In order to make that determination, Rachel
must make two separate (in Rachel's time) measurements of the interval between her and Bob.
Agree?
Who said you can't distinguish between (t,x) and (-t,-x)?
I'm pretty sure
I can, but I think I'd need more information than the diagram provides.
again, you shouldn't speak a rotation by some angle about an axis here. If we're sticking to the 2-d picture, then all rotations are in the x-t plane and are not about either axis.
O.K. We'll limit ourselves to rotations about an axis that doesn't exist.

If we're thinking of the full 4-d space, then rotations cannot be defined about an axis, at least not by one angle.
Not to be facetious, but is there some reasoning behind that assertion? Although it's not obvious to me how a rotation about a 4-vector might manifest itself, I certainly do not know that it cannot be characterized by a single angle.
Okay, I think I've figured out what you mean, although your language is a little imprecise (a capital offense in math, of course

).
I'm just a dumb engineer - don't bother suing me for heresy.

A distance does not have a direction - it's a scalar value. That's what it means that it's positive-definite, i.e. the absolute value.
The term "radius" is commonly construed as being positive-definite, but it is not. Positive radius in one direction is equivalent to negative radius in the opposite direction. I'll have to take another look at what I wrote to try and figure out why you don't think I understand this...
what freedom do you have left once you decide to hold one axis fixed? In 4-d, you still have 3 dimensions to play with, so saying "rotate by angle theta about the x-axis" is undefined.
Hey - I
like freedom. In fact, I think we need more! (knyuk-knyuk)
Rather than lump my assumptions into some [hopefully not] amorphous blob, let me try to put my "math-hat" on and be as explict as I can with what follows.
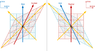
Let us start with the diagram of Bob's frame that DrGreg so graciously provided.
Let me define a quantity "R" that represents a positive-definite (ack!) quantity composed by taking the RSS of the "space" and "time" components of some event in Bob's frame (relative to O, at some time t).
Let me define a quantity "r" that represents the absolute value of "space" relating some event (Rachel) to Bob's frame at time t.
Let me define a pseudo-spherical \theta - \phi coordinate system about O where:
\theta=sin^{-1} (\frac{\delta r}{\delta R})
\phi=tan^{-1} (\frac{\delta R}{\delta r})
From the diagram, I infer that Rachel's velocity (v) is 0.5 (c) relative to Bob since she exhibits half the displacement of a photon over any given time interval (someone should make it clear that "time" = ct rather than t in the diagram, but I digress...). Hence, I can assume that R_R=0.5ct (versus R_B=t). Using the definitions of \theta and \phi supplied above, I infer that r_R=R_R sin(\theta), or r_R=\frac{R_R}{tan(\phi)}. Substituting for r_R yields:
sin(\theta)=\frac{1}{tan(\phi)}.
Although it is obvious that \theta is the angle between Bob and Rachel's (velocity) vectors on the diagram, it may be less clear what the \phi I've defined relates to. To illustrate, draw a horizontal line at some non-zero t across the diagram. Set a compass to a radius equal to the "space" between Rachel and Bob at time t, and then draw an arc about Bob's position that passes through Rachel's world-line at two different points. The more negative time point is where Bob observes Rachel at time t, and the more positive point is Rachel's Lorentz corrected position. More succintly, \phi is the angle between the observed position and projected position at time t in Bob's (time-travelling) frame.
-----
"math-hat" off...
In relation to Maxwell's equations, there are two operators that I feel are relavant to this discussion: curl and divergance. If I were to draw a circle of radius R=ct about O in Bob's frame, divergence could be represented as a radial vector toward any point on the circle. The curl at any point can then be construed as a unit vector tangential to a circle of radius R, and perpendicular to \vec R. In order to express divergence as a unit vector, we have div=\frac{\vec R}{ct}. Hence, if I posit that Maxwell's equations apply to closed
spherical surfaces, then "time" and "div" are parallel - and curl is perpendicular to "time".
BTW - You may note that drawing a circle corresponding to Bob's distance from O bisects the two points on Rachel's world line identified earlier...
Regards,
Bill
P.S. I hope I don't look too much like the tropicana girl with my "math-hat" on.