- #1
zenterix
- 480
- 70
- TL;DR Summary
- I'd like to understand a section of a book I am reading ("Introduction to Special Relativity" by Resnick).
I will create a series of posts that go through snippets of the section "relativistic kinematics" of the book and try to interpret the content in my own words and perform certain calculations that were left for the reader to do.
I'm going to go step-by-step through the reasoning. If there is any mistake, then it is a true mistake because I am trying to make each statement that follows as accurate as I can.
Unambiguous time scale in a single frame of reference.
Consider that we have two inertial frames of reference, 1 and 2.
We also have two events, A and B.
1) If the two events occur at the same location in space, then one clock in frame 1 at that location can tell us if the events are simultaneous in that frame.
2) If two events occur at different locations in space in frame 1, and if we have one clock in each location, we need to make sure the clocks are synchronized.
The book seems to be mixing the names of the events here (A and B) with the names of the observers (ie, frames).
Spelling everything out with maximum detail I think this means the following
1) Observer A is a reference frame with origin at the space location of event A and at rest relative to this location.
2) Observer B is a reference frame with origin at the space location of event B and at rest relative to this location.
Since the space locations of events A and B are at rest relative to one another, then the frames of reference of observers A and B are also at rest relative to each other.
Let me try to show this result.
Observer A is at the location of event A and suppose the clock says zero.
A light ray takes ##L/c## to arrive from the location of event B.
Observer A "seeing" the clock at event B means that he sees light arriving from clock B (presumably through a telescope).
Thus, for observer A to see the clock at event B showing zero when clock A is showing zero, the light ray had to leave event B (showing time zero) when clock A time was ##-L/c##.
Thus, the clocks are not really synchronized: observer A simply sees the clocks as showing the same time at any given time in his frame, but he is actually seeing the time at clock B at ##L/c## in the past: clock B is really ahead by ##L/c##.
Now, whenever light moves from clock A to clock B, it starts at a time that is ##L/c## behind clock B and then takes ##L/c## to arrive, so that when it arrives it is ##2L/c## behind clock B.
Thus observer B observes clock A to be ##2L/c## behind clock B.
Here is a pictorial depiction of this
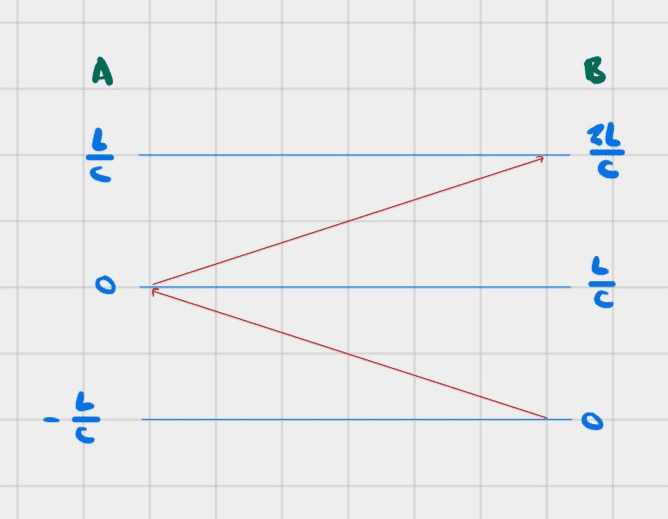
One question I have is about the statement
Is it technically correct that observers A and B are in the same frame?
I mean, I can see that the only difference between their frames is a constant term. It just bothers me to say they are the same frame. Are they?
The conclusion here is that if the definition of synchronized clocks is that one of the observers sees the clocks as showing the same time, then other observers in frames at rest relative to the first observer will not see the clocks as showing the same time.
Unambiguous time scale in a single frame of reference.
Consider that we have two inertial frames of reference, 1 and 2.
We also have two events, A and B.
1) If the two events occur at the same location in space, then one clock in frame 1 at that location can tell us if the events are simultaneous in that frame.
2) If two events occur at different locations in space in frame 1, and if we have one clock in each location, we need to make sure the clocks are synchronized.
Some "obvious" methods of synchronizing clocks turn out to be erroneous. For example, we can set the two clocks so that they always read the same time as seen by observer A. This means that whenever observer A looks at the B clock it reads the same to him as his clock.
The book seems to be mixing the names of the events here (A and B) with the names of the observers (ie, frames).
Spelling everything out with maximum detail I think this means the following
1) Observer A is a reference frame with origin at the space location of event A and at rest relative to this location.
2) Observer B is a reference frame with origin at the space location of event B and at rest relative to this location.
Since the space locations of events A and B are at rest relative to one another, then the frames of reference of observers A and B are also at rest relative to each other.
This means that whenever A looks at the B clock it reads the same to him as his clock. The defect here is that if observer B uses the same criterion (that is, that the clocks are synchronized if they always read the same time to him), he will find that the clocks are not synchronized if A says that they are. For this method neglects the fact that it takes time for light to travel from B to A and vice versa. The student should be able to show that, if the distance between the clocks is ##L##, one observer will see the other clock lag his by ##2L/c## when the other observer claims that they are synchronous. We certainly cannot have observers in the same reference frame disagree on whether clocks are synchronized or not, so we reject this method.
Let me try to show this result.
Observer A is at the location of event A and suppose the clock says zero.
A light ray takes ##L/c## to arrive from the location of event B.
Observer A "seeing" the clock at event B means that he sees light arriving from clock B (presumably through a telescope).
Thus, for observer A to see the clock at event B showing zero when clock A is showing zero, the light ray had to leave event B (showing time zero) when clock A time was ##-L/c##.
Thus, the clocks are not really synchronized: observer A simply sees the clocks as showing the same time at any given time in his frame, but he is actually seeing the time at clock B at ##L/c## in the past: clock B is really ahead by ##L/c##.
Now, whenever light moves from clock A to clock B, it starts at a time that is ##L/c## behind clock B and then takes ##L/c## to arrive, so that when it arrives it is ##2L/c## behind clock B.
Thus observer B observes clock A to be ##2L/c## behind clock B.
Here is a pictorial depiction of this
One question I have is about the statement
We certainly cannot have observers in the same reference frame disagree on whether clocks are synchronized or not, so we reject this method.
Is it technically correct that observers A and B are in the same frame?
I mean, I can see that the only difference between their frames is a constant term. It just bothers me to say they are the same frame. Are they?
The conclusion here is that if the definition of synchronized clocks is that one of the observers sees the clocks as showing the same time, then other observers in frames at rest relative to the first observer will not see the clocks as showing the same time.