Understanding Transformer Phasor Diagrams

[Peter Alexander]

Hello everyone! I'm currently studying transformers and a task related to phasor diagrams shows up. I'm having lots of problems with comprehension of the subject, so I'd like to ask for some help. I don't understand how the phasor diagram given as a solution could possibly be drawn out of the computed data.

1. The problem statement, all variables, and given/known data
Task gives the following data:

• $S_n = 1\text{MVA}, \quad 10\text{kV} / 0.4\text{kV}, \quad f=50\text{Hz}$
• $P_{Cun} = 15\text{kW}, \quad P_0 = 5\text{kW}$
• $u_K = 6\text{%}$
• Current through the secondary coil $I_2 = 1000A$ at $\cos{\phi_2} = 0.5$, inductive

And requires computation of losses in copper on secondary side (this represents windings), iron (this represents the core) as well as actual value of $U'_2$.

Homework Equations

All relevant equations will be present in the attempt at a solution.

The Attempt at a Solution

I believe that it's best for the solution to come in sequential steps instead of a long essay.

1. Compute the rated currents $I_{1n} = \frac{S_n}{U_1\sqrt{3}} = 57.34\text{A}$ and $I_{2n} = \frac{S_n}{U_2\sqrt{3}} = 1443.4\text{A}$
2. Winding losses for secondary coil are therefore $P_{Cu} = P_{Cun}\cdot (\frac{I_2}{I_{2n}})^2 = 7200\text{W}$
3. Core losses are computed as $P_{Fe} = P_{Fen}\cdot\frac{f'}{f_n}\cdot(\frac{B'}{B_n})^2$ but since $U_1' = 1.1 U_1$ we can deduce that $f'B' = 1.1 f_n B_n$ consequently leading to $P_{Fe}=P_{Fen}\cdot\frac{f'}{f_n}\cdot (1.1\cdot\frac{f_n}{f'})^2 = 5042\text{W}$
4. As a result, $E_2' = 1.1 \cdot U_2 = 1.1 \cdot E_2n = 440\text{V}$
5. For $U'_2$, we need the following values: $u_K = 6\text{%}$, $u_R = \frac{P_Cun}{S_n} = 1.5\text{%}$ and $u_X = \sqrt{u_K^2 - u_R^2} = 5.81\text{%}$.
6. We require a ratio $\frac{I_2}{I_{2n}} = 0.6929$ which is preserved even on the primary side, making $I_1 = 0.6929 \cdot I_{1n} = 39.73\text{A}$.
   
7. From here on, I'm starting to get lost. From known ratio, we can compute $u'_R = 1.039\text{%}$, $u'_X = 4.025\text{%}$ and $u_K = 4.157\text{%}$, where all we did was to multiply previous values by the factor $0.6929$.
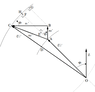
8. This equation is given on the datasheet and it describes the voltage drop on secondary side $\Delta U$. It can also be derived from the Kapp triangle using points on the diagram (will attach it below). Computational procedure is $$\Delta U = U_2 \cdot (
   u'_{R}\cos\phi_{2}+u'_{X}\sin\phi_{2}+U_{1}-\sqrt{U_{1}^{2}-(u'_{X}\cos\phi_{2}-u'_{R}\sin\phi_{2})^{2}}\cong4\text{\%}) = 17.6\text{V}$$ meaning that $U'_2 = E'_2 - \Delta U = 422.4\text{V}$

Now if we take a look at the phasor diagram (should be attached below), proportions don't add up, because if $U'_1 = 1100\text{V}$, then how can $U'_2$, which should be $422.4\text{V}$, be drawn as if it measures $\approx 660\text{V}$?

Any sort of help would me more than appreciated.

 

[Babadag]

From the attached Single-Phase Transformer Diagram where:
Vp=primary rated voltage
Rp=primary windings resistance
Xp=primary windings magnetic flux leakage reactance
Xm= main magnetic flux reactance
Rfe= equivalent resistance of magnetic losses
Ip=primary load current
Io=primary windings main magnetic flux current
I's=secondary current referred to primary
V's=secondary terminals voltage referred to primary
R's=secondary windings resistance referred to primary
X's=secondary windings leakage reactance referred to primary
E1=e.m.f of primary windings
E'2=e.m.f. of seconadry windings referred to primary [E'2=E1]
Zp=Rp+jXp ; Z's=R's+jX's
Po=Rp*Io^2+E1^2/Rfe where E1^2/Rfe=Pcore
Pcore=Core loss = Hysteresis loss + Eddy current loss
Pcore=Kh.f.Bmax^n+Ke.f2.Bmax^2
If we could neglect Rp*Io^2 then Po=Pcore
If we shall neglect hysteresis loss then only eddy current loss will be:
Po=Ke.f^2.Bmax^2
Bmax=k.E1/f/Areacore
Po/Pon=Ke.f^2.Bmax^2/Ke.f^2.Bmax^2=(f/fn*Bmax/Bmaxn)^2 or:
Po/Pon=[f/fn.E1/E1n.fn/f]^2=(E1/E1n)^2
E=Vp-Zp*Ip=V's+Z's*I's
In order to calculate E we need to know Zp or Z's.
In a short-circuit case E1=E2≈0 then Zsc=Zp+Zs'
Zsc=Vp^2/S.uk%/100
So what we can know it is only Zsc and we don't know what is Zp and Zs' separate.
Let's say Zp=Z's=Zsc/2
Now we could calculate E1/E1n and recalculate Po.
The resistance and reactance it could be considered constant.

 

[Babadag]

 

[Peter Alexander]

This was actually incredibly helpful! Thank you for your time and patience! I finally understand how it works, thank you!