ddddd28
- 73
- 4
Is it always true that:
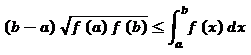
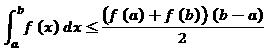
Noticing that it works for some functions, I wanted to ensure it is true for all of them( at least polynomical), but since I am still in high school, and I don't have deep understanding in calculus( yet), the question is forwarded to you. proof please!
Noticing that it works for some functions, I wanted to ensure it is true for all of them( at least polynomical), but since I am still in high school, and I don't have deep understanding in calculus( yet), the question is forwarded to you. proof please!
Attachments
Last edited by a moderator: