chwala
Gold Member
- 2,827
- 415
- Homework Statement
- A particle with mass ##0.4## kgs is projected with a speed of ##12## m/s up a line of greatest slope of a smooth plane inclined at ##30^0## to the horizontal.
i. Find the initial kinetic energy of the particle.
ii. Use an energy method to find the distance moved by the particle up the plane before coming to instantaneous rest.
- Relevant Equations
- kinetic energy
This is from an examination paper -A level. My interest is on part (ii). Ok my take;
i. ##KE_{initial} = \dfrac {1}{2} mu^2= \dfrac {1}{2}× 0.4 ×12^2=28.8## Joules.
ii. ##\dfrac {1}{2} mv^2=\dfrac {1}{2} mu^2-mgh##
##0=28.8-(0.4×10×h)## where h is the vertical perpendiculor distance.
##h=\dfrac{28.8}{4}=7.2##
It follows that;
##\sin 30^0=\dfrac{7.2}{s}##
##s=7.2×2=14.4## m
where ##s## is the distance travelled by the particle before coming to rest.
Your insight appreciated.
Mark scheme solution here
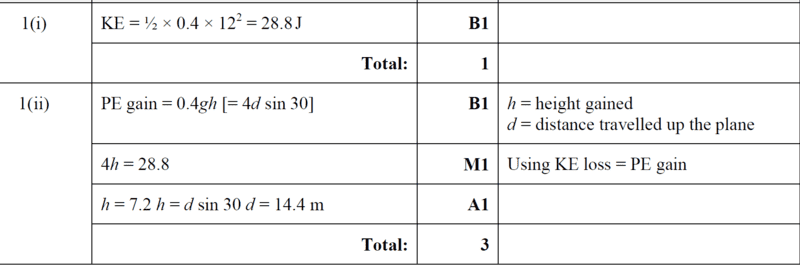
i. ##KE_{initial} = \dfrac {1}{2} mu^2= \dfrac {1}{2}× 0.4 ×12^2=28.8## Joules.
ii. ##\dfrac {1}{2} mv^2=\dfrac {1}{2} mu^2-mgh##
##0=28.8-(0.4×10×h)## where h is the vertical perpendiculor distance.
##h=\dfrac{28.8}{4}=7.2##
It follows that;
##\sin 30^0=\dfrac{7.2}{s}##
##s=7.2×2=14.4## m
where ##s## is the distance travelled by the particle before coming to rest.
Your insight appreciated.
Mark scheme solution here