Using Kirchhoff's Rules - Calculating Currents

[PeachBanana]

Homework Statement

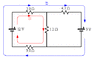
What currents are provided by the batteries? What is the voltage drop across the 1.2 Ω
resistor?

Homework Equations

V = IR
Junction Rule = sum of current at a junction = 0
Loop Rule = sum of changes in potential around any closed path of a circuit must be 0

The Attempt at a Solution

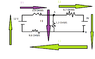
I hope what I've drawn is clear enough. I 1 only goes around the small rectangle whereas I 2 encompasses the entire rectangle.

The current provided by the 12 V battery using the loop rule:

12 V + (3.9 Ω)(I1)+(1.2 Ω)(I1) + (9.8 Ω)(I1) = 0

Does that make sense? I'm unsure when it comes to these rules.

 

[gneill]

When you "walk" around a loop doing a KVL sum, be sure to pay attention to the polarities of the potential changes. If you pass through a resistance in the same direction as the current, does the potential rise or drop? Also, it sounds as though you've specified that I2 also passes through the 3.9 and 9.8 Ohm resistors, so it must also contribute to the total potential change in those resistors.

 

[PeachBanana]

Okay I think I understand better. If the resistance is in the same direction as the current, that would be considered a voltage drop.

So really, I have two unknowns.

12 V - (3.9 Ω)(I1) - (1.2 Ω)(I1) - (9.8 Ω)(I1) - (3.9 Ω)(I2) - (9.8 Ω)(I2)= 0

So then maybe applying this same loop rule to I2 I would have:

(3.9 Ω)(I2) - (3.9 Ω)(I1) - (6.7 Ω)(I2) - 9V - (9.8 Ω)(I2) - (9.8 Ω)(I1) + 12 V = 0

 

[gneill]

Okay I think I understand better. If the resistance is in the same direction as the current, that would be considered a voltage drop.

So really, I have two unknowns.

12 V - (3.9 Ω)(I1) - (1.2 Ω)(I1) - (9.8 Ω)(I1) - (3.9 Ω)(I2) - (9.8 Ω)(I2)= 0

So then maybe applying this same loop rule to I2 I would have:

(3.9 Ω)(I2) - (3.9 Ω)(I1) - (6.7 Ω)(I2) - 9V - (9.8 Ω)(I2) - (9.8 Ω)(I1) + 12 V = 0

Yup. Just verify the sign of the first term in the loop 2 equation. Otherwise, nicely done.

 

[Nickie]

Based on the given circuit, there are two batteries providing current: the 12V battery and the 4.9V battery. Using the junction rule, the total current at the junction where the two batteries are connected must be 0. Therefore, the current provided by the 12V battery must be equal to the current provided by the 4.9V battery.

To calculate the current provided by the 12V battery, we can use the loop rule. We can set up a loop starting at the positive terminal of the 12V battery, going through the 3.9Ω resistor, the 1.2Ω resistor, and back to the negative terminal of the 12V battery. The loop rule states that the sum of the changes in potential around any closed path of a circuit must be 0. Therefore, we can write the following equation:

12V + (3.9Ω)(I1) + (1.2Ω)(I1) = 0

Solving for I1, we get a current of approximately 2.24A provided by the 12V battery.

To calculate the voltage drop across the 1.2Ω resistor, we can use Ohm's Law, V = IR. We know the current through the resistor (I1 = 2.24A), so we can plug that in and solve for V:

V = (2.24A)(1.2Ω) = 2.69V

Therefore, the voltage drop across the 1.2Ω resistor is approximately 2.69V.

In summary, the 12V battery provides a current of 2.24A and the voltage drop across the 1.2Ω resistor is 2.69V. It's always important to double check your calculations and make sure they make sense in the context of the circuit.