ainster31
- 158
- 1
Homework Statement
Homework Equations
The Attempt at a Solution
I understand how they calculated NPW but how did they use the linear interpolation method?
ainster31 said:Homework Statement
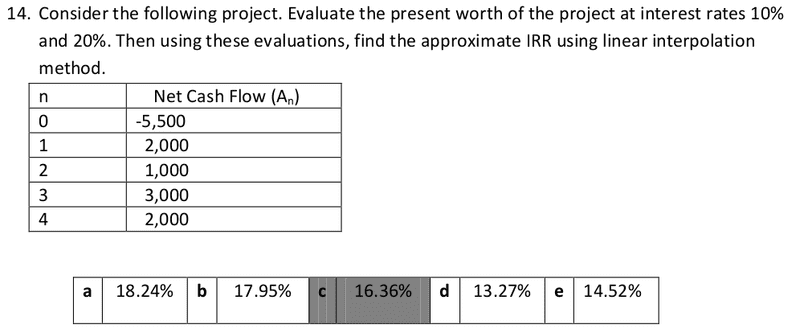
Homework Equations
The Attempt at a Solution
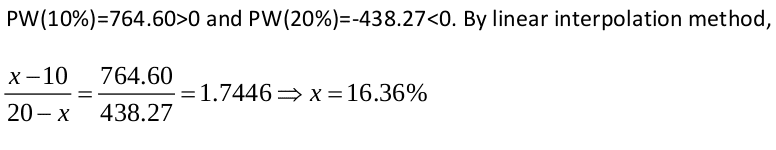
I understand how they calculated NPW but how did they use the linear interpolation method?
Ray Vickson said:That is not how I would do it, but it is correct.
ainster31 said:How would you do it? Just set f(x)=0 and solve for x?
Ray Vickson said:I already gave you the formula I would use:
x_0 = \frac{f_2 x_1 - f_1 x_2}{f_2 - f_1}
and I already explained how I got it.
ainster31 said:Homework Statement
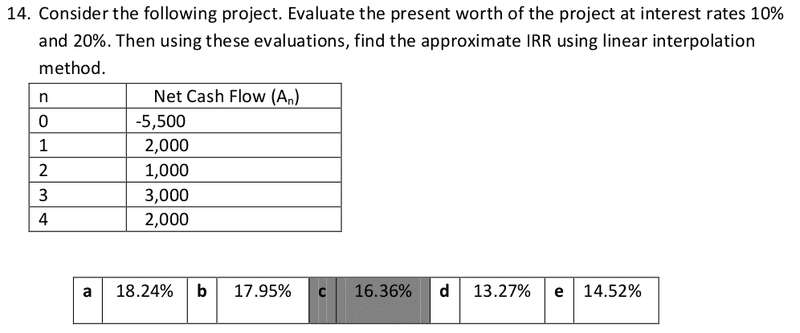
Homework Equations
The Attempt at a Solution
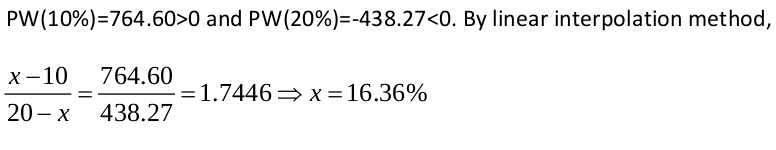
I understand how they calculated NPW but how did they use the linear interpolation method?