SUMMARY
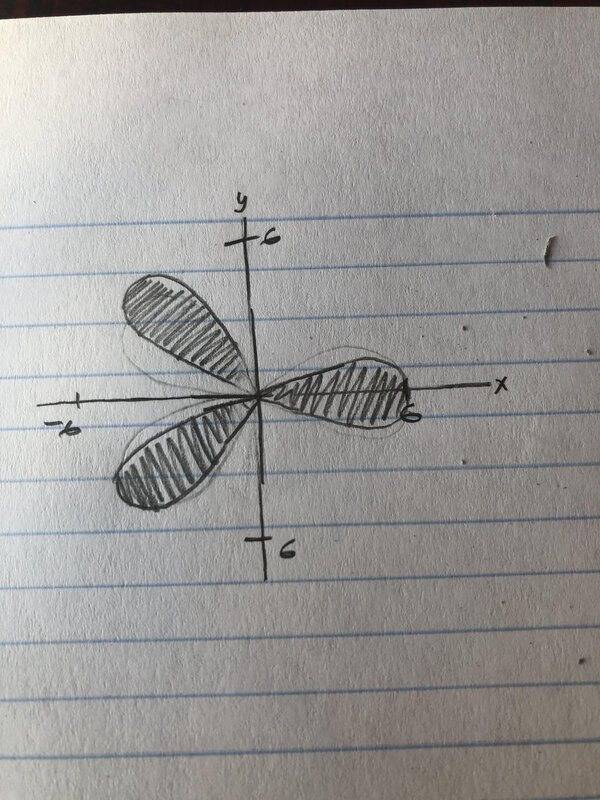
The discussion focuses on describing rose petals using polar coordinates, specifically the equation R = {(r, θ): 0 ≤ r ≤ 6 cos(3θ), 0 ≤ θ ≤ π}. The periodic nature of the function allows for the determination of additional petals by applying the phase shift r(θ + 2π/3) = r(θ). This periodicity means that once one petal is drawn, the others can be derived through this transformation, demonstrating the relationship between polar and Cartesian coordinates.
PREREQUISITES
- Understanding of polar coordinates and their equations
- Knowledge of periodic functions and phase shifts
- Familiarity with trigonometric functions, specifically cosine
- Basic concepts of Cartesian coordinates and their transformations
NEXT STEPS
- Explore the properties of polar coordinates in depth
- Learn about the graphical representation of polar equations
- Study the implications of periodicity in trigonometric functions
- Investigate transformations between polar and Cartesian coordinates
USEFUL FOR
Mathematicians, educators, and students studying polar coordinates and trigonometric functions, particularly those interested in graphical representations and transformations in mathematics.