outxbreak
- 30
- 0
1. The question asks you to determine whether the loop will rotate clockwise, counter clockwise, or not at all when viewed from above the loop along the indicated axis.
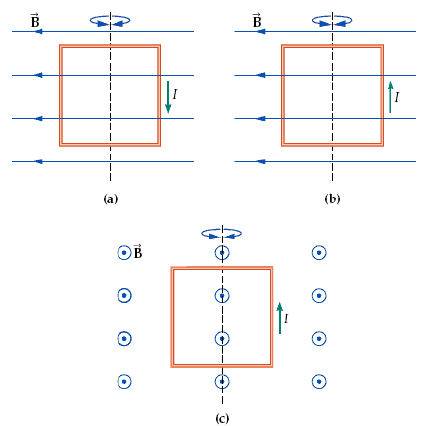
The book's strategy: The magnetic field exerts a force on each side of the
square current loop. Use the Right-Hand Rule (RHR) for the
magnetic force exerted on a current-carrying wire to determine the
directions the forces are exerted, and then use the RHR for
torques to determine the direction that the loop would rotate.
3. The book's solution
Solution: 1. (a) The force on the left vertical wire is out of the
page; the force on the right vertical wire is into the page; the
horizontal wires experience zero force. As a result, the loop tends
to rotate counterclockwise, as viewed from above.
2. (b) The force on the left vertical wire is into the page; the force
on the right vertical wire is out of the page; the horizontal wires
experience zero force. As a result, the loop tends to rotate
clockwise, as viewed from above.
3. (c) The force on the left vertical wire is to the left; the force on the right vertical wire is to the right; the force on the
top horizontal wire is upward; the force on the bottom horizontal wire is downward. As a result, there is no net force on
the loop and no net torque, so the loop will not rotate at all.
I understand how they determine the forces but have NO clue how they determine which way the loop rotates! :( The book does not talk about the RHR for torque in enough depth for me to figure this out.
The book's strategy: The magnetic field exerts a force on each side of the
square current loop. Use the Right-Hand Rule (RHR) for the
magnetic force exerted on a current-carrying wire to determine the
directions the forces are exerted, and then use the RHR for
torques to determine the direction that the loop would rotate.
3. The book's solution
Solution: 1. (a) The force on the left vertical wire is out of the
page; the force on the right vertical wire is into the page; the
horizontal wires experience zero force. As a result, the loop tends
to rotate counterclockwise, as viewed from above.
2. (b) The force on the left vertical wire is into the page; the force
on the right vertical wire is out of the page; the horizontal wires
experience zero force. As a result, the loop tends to rotate
clockwise, as viewed from above.
3. (c) The force on the left vertical wire is to the left; the force on the right vertical wire is to the right; the force on the
top horizontal wire is upward; the force on the bottom horizontal wire is downward. As a result, there is no net force on
the loop and no net torque, so the loop will not rotate at all.
I understand how they determine the forces but have NO clue how they determine which way the loop rotates! :( The book does not talk about the RHR for torque in enough depth for me to figure this out.