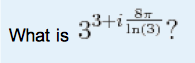SUMMARY
The discussion centers on evaluating the expression involving complex numbers, specifically 3 raised to the power of 3 plus a complex component. The calculations reveal that 3^(3 + i(8π/ln(3))) simplifies to 27, utilizing Euler's identity. The final result confirms that the expression evaluates to the real number 27, demonstrating the application of logarithmic properties and complex exponentiation.
PREREQUISITES
- Understanding of complex numbers and their properties
- Familiarity with Euler's identity and exponential functions
- Knowledge of logarithmic functions, particularly natural logarithms
- Basic algebraic manipulation of exponential expressions
NEXT STEPS
- Study Euler's identity in depth to understand its applications in complex analysis
- Learn about the properties of logarithms and their role in simplifying complex expressions
- Explore complex exponentiation techniques and their implications in various mathematical contexts
- Investigate the relationship between complex numbers and trigonometric functions
USEFUL FOR
Mathematicians, physics students, and anyone interested in complex analysis or exponential functions will benefit from this discussion.