- 1,277
- 1,078
Here is an interesting problem (in my opinion at least)
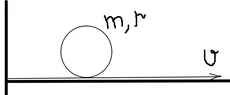
A rubber band is placed on a horizontal table and attached to a vertical wall by its left end. A disk of given mass and radius is placed on the band without initial velocity. Then the right end of the band is being drawn with constant speed ##v##. Find the motion of the disk.
It turns out that the kinetic energy of the disk vanishes as ##t\to \infty## while the disk rolls away in the right direction to infinity .
The disk does not slip. Very simple but nonholonomic problem by the way.
Original Sacharov's problem: a bug creeps to the right along the band with a speed ##u## wrt the band. Will the bug catch up a hand which draws the end of the band?
Hope I remember it correctly.
A rubber band is placed on a horizontal table and attached to a vertical wall by its left end. A disk of given mass and radius is placed on the band without initial velocity. Then the right end of the band is being drawn with constant speed ##v##. Find the motion of the disk.
It turns out that the kinetic energy of the disk vanishes as ##t\to \infty## while the disk rolls away in the right direction to infinity .
The disk does not slip. Very simple but nonholonomic problem by the way.
Original Sacharov's problem: a bug creeps to the right along the band with a speed ##u## wrt the band. Will the bug catch up a hand which draws the end of the band?
Hope I remember it correctly.
Attachments
Last edited: