- #1
brentwoodbc
- 62
- 0
Homework Statement
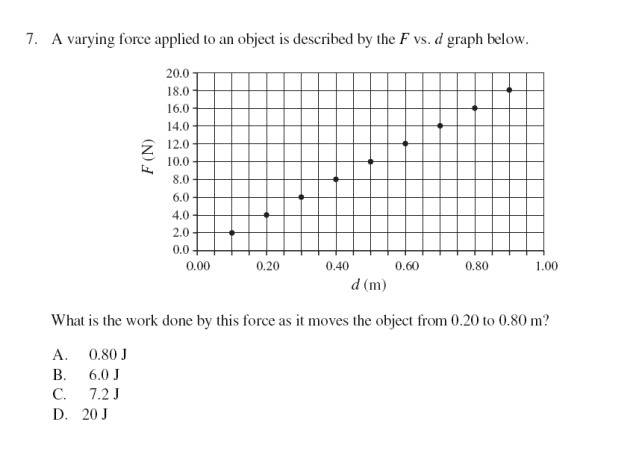
I get an answer of 7.2, it says the answer is supposed to be 6.
I do w=fd
w=(16-4)x(.8-.2)
w=12x.6
w=7.2?
thanks.
Varying force is applied to an object problem
Click For Summary
The calculation of work done on an object with varying force requires summing the contributions of force over distance rather than using a simple difference between starting and ending forces. The correct approach involves integrating the force function or approximating it with a piece-wise continuous model. The initial calculation resulting in 7.2 is incorrect because it does not account for the varying nature of the force. For those familiar with calculus, integrating the force function over the specified interval will yield the correct total work. Understanding the principles of variable force is essential for accurately solving this type of problem.
I get an answer of 7.2, it says the answer is supposed to be 6.
I do w=fd
w=(16-4)x(.8-.2)
w=12x.6
w=7.2?
thanks.
- #2
berkeman
Admin
- 69,302
- 24,529
brentwoodbc said:Homework Statement
I get an answer of 7.2, it says the answer is supposed to be 6.
I do w=fd
w=(16-4)x(.8-.2)
w=12x.6
w=7.2?
thanks.
The force is varying with distance, not a constant diffrerence of the ending and starting force. You will need to add up all the little F*d contributions to get the total work. You could write an equation for the line, the F(d) line, or you could approximate it as a piece-wise continuous stair-step waveform.
If you have used calculus in your course so far, write the equation for the line and do the integration to sum up the F(d) over the interval. If you haven't use integration for this before, just do the sum for each little interval you see on the graph between the endpoints that they are asking about.
Similar threads
- · Replies 3 ·
- · Replies 11 ·
- · Replies 11 ·
- · Replies 16 ·
- · Replies 12 ·
- · Replies 2 ·